The starmaze is a hall of mirrors. Every pattern is surrounded by a kaleidoscope of reflections and rotations and inversions that make simple relationships seem more complex than they really are. Forms are an attempt to reduce that kaleidoscope to something more manageable. In particular, this page shows how forms can uncover the common structure lurking beneath the thousands of varied solutions to the original starmaze puzzle.
Each form consists of all the unique rotations and inversions of a pattern with and without an open center cell. By clumping together these rotations and inversions, the 512 different starmaze patterns are reduced to one of 20 basic forms.
Most forms include a total of 32 patterns - 8 basic rotations, doubled once to include a flipped center cell and doubled again to include all the inverses. The more symmetrical patterns have fewer unique rotations and so include fewer patterns. Three of the forms have only 4 unique rotations, one form has only 2 rotations, and the final two forms have only 1 rotation.
The forms are arranged in order of the number of stars (open cells) in the initial pattern. The first form has one star, forms 2 to 5 have two stars, forms 6 to 12 have three stars, forms 13 to 19 have four stars, and the final form has no stars.
Every movement within the maze causes a transformation of one form into another. Each form can change into 2 to 9 other forms. Only 4 of the 20 forms can change into themselves. The transformations are commutative; if A can transform into B, then B can transform into A. Forms 7 and 8 are reflections of each other; each can transform into its reflection and to the same set of other forms. The same is true of forms 9 and 10. So both of these pairs are combined in the following transformation chart:
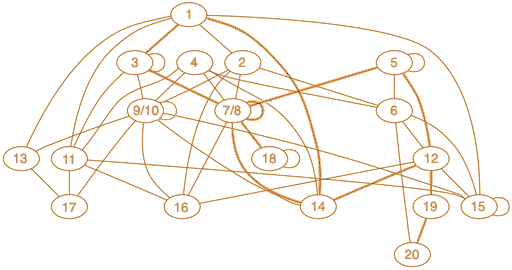
The bold edges indicate which transformations are involved in the solution to the starmaze puzzle. There are a total of 1920 different solutions, but when the various rotations are collapsed to their underlying forms, the total number of solutions can be reduced down to 20 variations, which can then be captured in a single diagram:
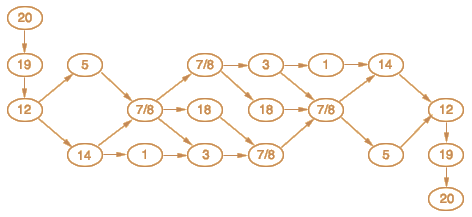
| Form Sequence | Solutions |
|---|---|
|
20-19-12-05--78-03-78-78--05-12-19-20 20-19-12-05--78-03-78-78--14-12-19-20 20-19-12-05--78-78-03-01--14-12-19-20 20-19-12-05--78-78-03-78--05-12-19-20 20-19-12-05--78-78-03-78--14-12-19-20 20-19-12-05--78-78-18-78--05-12-19-20 20-19-12-05--78-78-18-78--14-12-19-20 20-19-12-05--78-18-78-78--05-12-19-20 20-19-12-05--78-18-78-78--14-12-19-20 20-19-12-14--01-03-78-78--05-12-19-20 20-19-12-14--01-03-78-78--14-12-19-20 20-19-12-14--78-03-78-78--05-12-19-20 20-19-12-14--78-03-78-78--14-12-19-20 20-19-12-14--78-78-03-01--14-12-19-20 20-19-12-14--78-78-03-78--05-12-19-20 20-19-12-14--78-78-03-78--14-12-19-20 20-19-12-14--78-78-18-78--05-12-19-20 20-19-12-14--78-78-18-78--14-12-19-20 20-19-12-14--78-18-78-78--05-12-19-20 20-19-12-14--78-18-78-78--14-12-19-20 |
256 128 64 256 128 128 64 128 64 64 32 128 64 32 128 64 64 32 64 32 |
| 1920 |
The symmetry of the solution is apparent here. As described in Reading the Solution, the overall path involves going into the maze, turning around, and coming back out. As this diagram reveals, there are several basic ways to "turn around", but they all involve a transformation from 7/8 to 7/8, which is actually either 7 to 8 or 8 to 7.
What is so special about form 7 and 8? For one thing, these two forms, along with forms 9 and 10, are the only forms which exhibit the property of chirality (handedness). All the other forms contain their own horizontal or vertical reflections. That is, any one of their patterns can be reflected by either rotating or inverting. For this reason, these other forms are said to be achiral.
Patterns in form 7, on the other hand, have an asymmetric distribution of open cells that cannot be reflected by rotation or inversion. Instead, each pattern in form 7 has its reflection in form 8 and vice versa. Moreover, by moving through the center cell, it is possible to transform directly between forms 7 and 8. This particular transformation creates the fulcrum across which every solution balances.
Let's look at the classic solution path as an example:
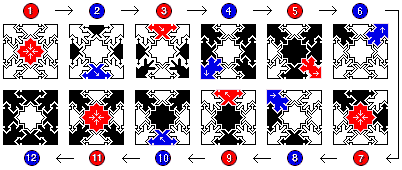
The first four patterns (going into the maze) are of forms 20, 19, 12, and 5. The last four patterns (coming back out) are the same four forms in reverse. The four middle patterns (turning around) are of form 8, 3, 8, and 7. If you check the solution diagram above, you can verify that 20-19-12-05-08-03-08-07-05-12-19-20 is indeed the first of the 20 possible form sequences.
Each of the 1920 possible solutions begin and end with a move through the center, and they all include a third center move somewhere in between. That middle center move is always a transformation from a form 7 pattern to a form 8 pattern (or vice versa) and this transformation always changes the chirality. If you look carefully, you will see that the transformation from pattern 7 to 8 in our above example is indeed a transformation from a right-handed form to a left-handed form.
The form 7 and 8 patterns involved in the solution all occur in rooms c or i in every other microcosm (Bc, Bi, Dc, Di, Ec, Ei, etc.) as shown here on the original starmap:
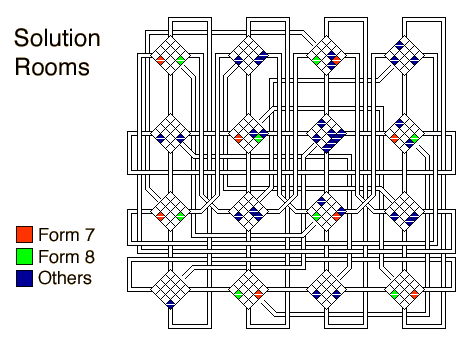
The solution can be described as finding a blue path to a red or green room, traveling through a center-pipe from green to red or red to green, then taking blue rooms back out the way you came. Notice that there are no free triangles; all the triangular rooms occur only in diamond-shaped pairs. This means that if any pattern participates in a solution, than its inverse does too.
Because each starmaze form includes both patterns and their inverses with and without the center cell open, all patterns of a given form emanate the same number of rings. For more information, see Cycles and Seasons. Each form includes patterns of up to four different elements. The Elements page contains a diagram showing how the five elements correlate to the twenty forms.
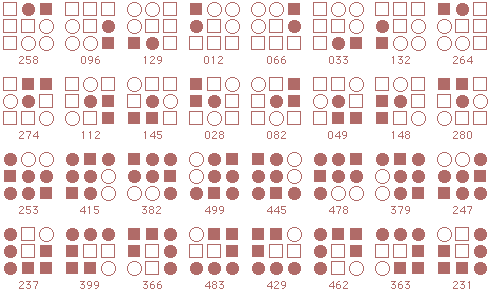
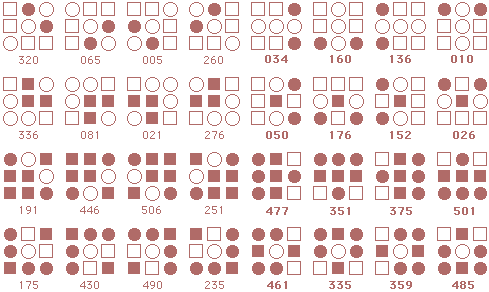
Following is a complete listing of starmaze forms. Each form is arranged in four rows of patterns.
The first row contains rotations with the center cell closed: first the
0, 90, 180, and 270 degree rotations, then the 45, 135, 225, and 315 degree rotations.
The second row is the same rotations with the center cell open. Rows three and four are inverses of the first two rows.
Room numbers participating in at least one variation of the solution are shown in bold.
![]()
Form 1: Distant Star
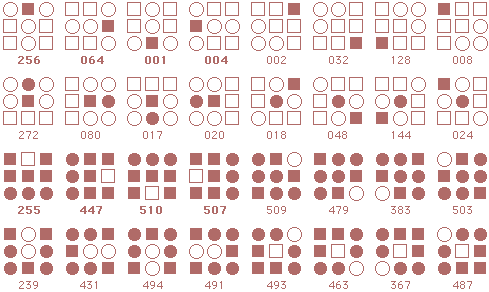
Form 2: Cranes
Form 3: Ravens
Form 4: Sun and Moon
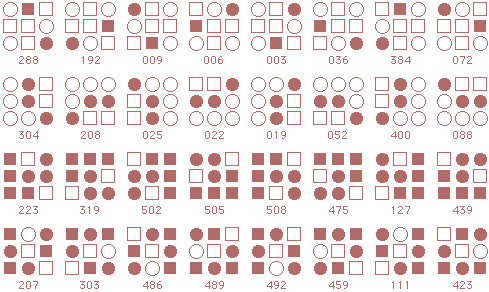
Form 5: Cranes Flying
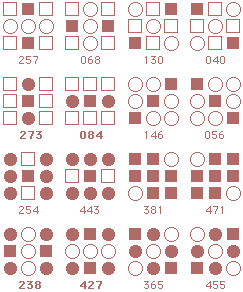
Form 6: Lion
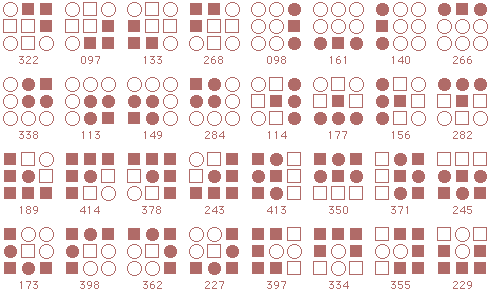
Form 7: Chasing Cranes Left
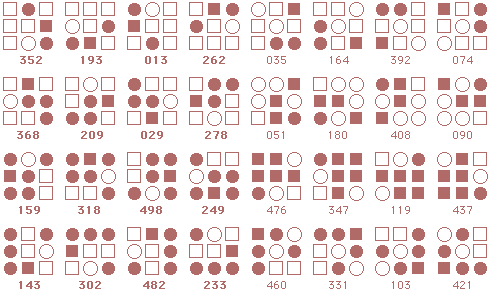
Form 8: Chasing Cranes Right
Form 9: Dancing Dog Left
Form 10: Dancing Dog Right
Form 11: Hidden Dragon
Form 12: Facing the Ravens
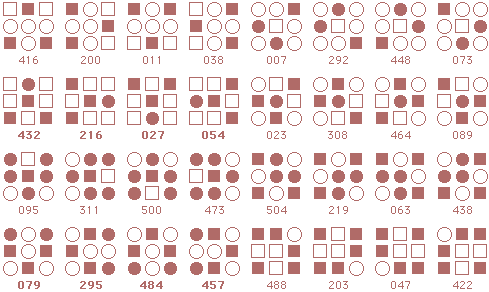
Form 13: Dragon Walking
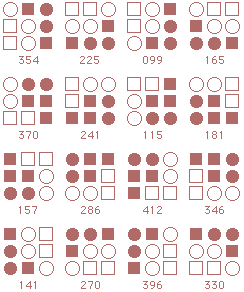
Form 14: Chasing the Lion
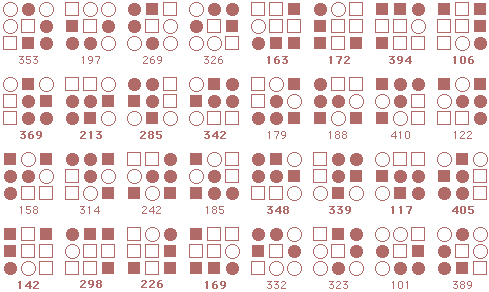
Form 15: Facing the Lion
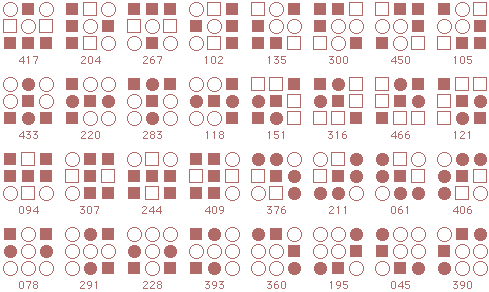
Form 16: Cranes and Ravens
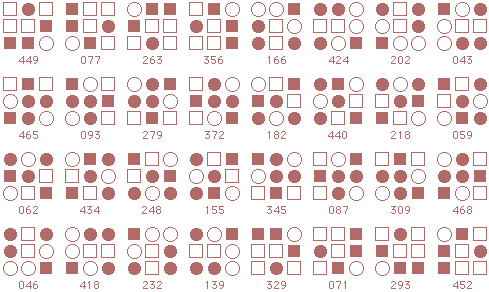
Form 17: Clouds
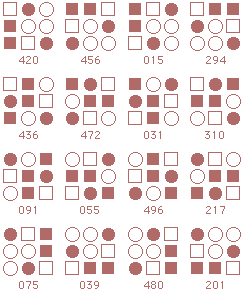
Form 18: Double Wedding
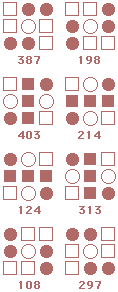
Form 19: Flying Dragon

Form 20: Eternal Moment