After years of study I gradually became aware that the starmaze is just one example of a larger class of structures I now call hypercube puzzles. So not only are there different orders or sizes of starmaze puzzle (5-D, 9-D, etc.), there are also for any given order, many different hypercube puzzles each with different behaviors and properties.
Each hypercube puzzle consists of a set of 2n patterns, one for each corner of the n-dimensional hypercube upon which it is based. Each pattern consists of n cells, each cell holding either a circle or a square for each 0 or 1 in that corner's binary address.
The circles and squares are either empty or filled depending on the direction of the edges coming to or going from each corner. If the corner's first dimensional edge is inbound, then the first cell's shape is empty. If the corner's second dimensional edge is outbound, then the second cell's shape is filled. And so forth.
A player can change one pattern to another by choosing any open (filled) cell. Choosing a particular cell is equivalent to choosing a particular outbound edge, which then leads to a new pattern. The cells in that new pattern will have the same sequence of circles and squares except for the chosen cell, which will flip from circle to square or square to circle. And since the outbound edge of the previous pattern is now an inbound edge to the new pattern, that circle or square will be empty.
This is where the similarities end. The assignment of the other filled and empty shapes in the new pattern will depend entirely on the unique nature of that particular puzzle. In some puzzles it is always possible to move from any pattern to any other pattern. Other puzzles have source patterns which, once left, can never be returned to, and sink patterns or "pits" from which one can never escape, or even source and sink regions that divide the puzzle into a fractured archipelago. Some puzzles have patterns with many different arrangements of open and closed cells. Some have only two possible arrangements.
All of this depends on the unique assignment of directions for each edge. This assignment is what defines most of the behavior of each different hypercube puzzle. This unique assignment is called the puzzle's "key".
A key consists of either a 0 or a 1 for each edge of the underlying hypercube; a filled square leading to an empty circle gets a 0, a filled circle leading to an empty square gets a 1. Since there are n2n-1 edges in an n-dimensional hypercube, there are n2n-1 digits in a puzzle key. For larger values of n it is convenient to represent the digits of a key in a graphical manner, by arranging the digits in a rectangular block and using black squares for 1s and white squares for 0s.
To understand how this works, let's first look at the simple example of a hypercube puzzle of order 3 - an ordinary cube. A cube has 8 corners and 12 edges. So a 3-cube puzzle will have 8 patterns of 3 cells each and a 12 digit key:
The edges of a key are numbered in a particular order. First come all the edges of the first dimension, then all the edges of the second dimension, and so forth. Within each dimension, the edges are numbered by removing the digit corresponding to that dimension and then evaluating the remaining digits as a binary number (least significant digits first) and using that number to determine the order.
So the key of this cube is 0110 0101 0011. There are a total of 212 = 4096 different possible order 3 hypercube puzzles, with keys ranging from 000000000000 to 111111111111. Converting from binary to decimal, we can say that this particular cube is number 1619.
Cube 1619 is a special cube. It's the 3-dimensional analog of the starmaze, as described in Other Dimensions. Like the starmaze, it has one source, one sink, and relatively few cycles (in this case only the one along the top face, which is 25% of the maximum four cycles possible in a cube).
Also like the starmaze, it has 100% coverage. "Coverage" is defined as the percentage of the maximum possible permutations of filled and unfilled cells occurring in the patterns of a particular hypercube puzzle. In a cube there are 8 possible permutations ranging from 000 (closed-closed-closed) to 111 (open-open-open). From here on, we'll restrict the word "pattern" to refer only to this numbered arrangement of open and closed cells.
If you look at the diagram of cube 1619 above, you will see that pattern 000 occurs in only one corner. Pattern 001 also occurs once and only once. And so on for all eight possible patterns. Since all 8 of the 8 possible patterns occur, cube 1619 has 8/8 or 100% coverage. This is why it has one source and one sink - these correspond to patterns 111 and 000. About 20% of all possible cubes have full coverage.
The distribution of coverage values in order 3 hypercube puzzles hints at the way coverage is distributed in higher dimensions:
1/8: 0
2/8: 8 = .2%
3/8: 0
4/8: 424 = 10.4%
5/8: 256 = 6.25%
6/8: 2592 = 63.28%
7/8: 0
8/8: 816 = 19.9%
Of the 4096 different cubes, none of them produce puzzles with only 1 or 3 or 7 patterns because adjacent patterns are not fully independent. Regardless of the other edge assignments, an outbound edge from one pattern is guaranteed to be the inbound edge of another, so any two neighboring patterns are always different. This immediately makes puzzles with only 1 pattern impossible (in puzzles of any size). And in the limited space of a cube it's just as impossible to have exactly 3 or exactly 7 patterns, though the precise reasons for this are more complicated.
Two patterns, then, is the minimum coverage possible in any order of hypercube puzzle. As our survey reveals, "minimum coverage" arrangements are quite rare. For cubes there are only 8 out of 4096.
The following diagram shows each of these 8 cubes flattened with diagonal lines representing the y (front/back) dimension. Each cube is numbered using the 12-digit key based on its edge directions. The even and odd corners of the cubes are represented by white and black circles respectively. In each cube, one pattern occurs in all its even corners (including its origin - position 000 in the lower left corner) and a second pattern occurs in all its odd corners; these two patterns are shown below each cube.
Two of these cubes, 1638 and 2457, consist of four sources leading to four sinks, so their patterns consist of either all open or all closed cells. The other six are the maximum cycle cubes discussed in Cycles and Seasons. Each has four cycles, the maximum number possible in a cube. Each of the first four patterns is the inverse of one of the last four; the inverse of any maximum cycle cube has cycles in the same faces but in opposite directions.
All 8 cubes have very similar key values, consisting of all possible triplets of just two binary strings: 0110 and 1001. Even more remarkable, when the 12-bit keys are reduced to 3-bit triplets (AAA, AAB, etc.) each triplet corresponds precisely to the patterns appearing in that cube's origin. 0110 is a special string called the "minimum coverage sequence" (discussed below). As we'll see, these properties help us to create minimum coverage keys in higher dimensions.
On the other end of the coverage spectrum, it was surprising to me that so many of these cube puzzles, nearly 20%, had full coverage. But this makes sense when you consider not just that all the rotations and reflections of a full coverage key also have full coverage, but also that even slightly mutated full coverage keys can still maintain full coverage. In cases in which two very similar patterns A and B are adjacent, switching a single edge direction between them can change A into B and B into A, resulting in no change of overall coverage. All of this helps us to understand that the starmaze's property of perfect coverage is not, in itself, a rare thing.
Slight coverage-neutral mutations can happen to a special set of keys called "neutral keys", the keys which consist of either all zeros or all ones in each dimension. In three dimensions there are eight possible neutral keys: all zeros in all three dimensions, all ones in dimension x and all zeroes in dimensions y and z, etc. The all-zeros neutral key produces a cube like this:
Notice that there are no empty squares or filled circles among the patterns. The all-zeros neutral key produces a puzzle in which there is no distinction between a pattern and its underlying binary address. As a result, each movement changes only a single cell and there are no cycles whatsoever. Instead, all edges flow irreversibly from the source to the sink in a structure I call a binary trickle. The all-ones neutral key has all the same properties except that its source and sink poles are reversed; the other six 3-D neutral keys are just additional rotations of this same basic structure.
Mutations in any one of the 12 edges would disrupt the unbroken flow from source to sink and cause the first appearance of a filled circle or empty square, but would not reduce the 100% coverage since adjacent patterns would simply swap their arrangement of filled and empty cells. Other mutations could also be added without reducing coverage, but as soon as two mutations are shared by the same corner, pattern duplications occur and the coverage rate begins to decline.
Every '1' digit in a key is a divergence from the all-zeros neutral key. On the other end of the spectrum, every '0' digit is a divergence from the all-ones neutral key. But in both cube 1619 and in the starmaze itself, exactly 50% of the key-digits in each dimension are ones, so in a sense they are as different as possible from neutral. Even so, the starmaze and its 3D analog are still able to provide 100% coverage because of the highly symmetrical way their edge "mutations" are distributed.
Order 9 Puzzle Keys
Comprehensive studies of cube puzzles are possible because the key to an order 3 puzzle has only 12 digits. The key to an order 9 puzzle like the starmaze is somewhat larger, 2304 digits in all:
0000000011111111111111110000000000000000111111111111111100000000 1111111100000000000000001111111111111111000000000000000011111111 0000000011111111111111110000000000000000111111111111111100000000 1111111100000000000000001111111111111111000000000000000011111111 0000000000000000000000000000000011111111111111111111111111111111 0000000000000000000000000000000011111111111111111111111111111111 1111111111111111111111111111111100000000000000000000000000000000 1111111111111111111111111111111100000000000000000000000000000000 0000111111110000000011111111000000001111111100000000111111110000 1111000000001111111100000000111111110000000011111111000000001111 0000111111110000000011111111000000001111111100000000111111110000 1111000000001111111100000000111111110000000011111111000000001111 0000111100001111000011110000111100001111000011110000111100001111 0000111100001111000011110000111100001111000011110000111100001111 1111000011110000111100001111000011110000111100001111000011110000 1111000011110000111100001111000011110000111100001111000011110000 0011001111001100110011000011001100110011110011001100110000110011 1100110000110011001100111100110011001100001100110011001111001100 0011001111001100110011000011001100110011110011001100110000110011 1100110000110011001100111100110011001100001100110011001111001100 0101010101010101010101010101010110101010101010101010101010101010 0101010101010101010101010101010110101010101010101010101010101010 0101010101010101010101010101010110101010101010101010101010101010 0101010101010101010101010101010110101010101010101010101010101010 0011001100110011110011001100110011001100110011000011001100110011 0011001100110011110011001100110011001100110011000011001100110011 0011001100110011110011001100110011001100110011000011001100110011 0011001100110011110011001100110011001100110011000011001100110011 0101101001011010010110100101101001011010010110100101101001011010 0101101001011010010110100101101001011010010110100101101001011010 0101101001011010010110100101101001011010010110100101101001011010 0101101001011010010110100101101001011010010110100101101001011010 0011001111001100110011000011001100110011110011001100110000110011 0011001111001100110011000011001100110011110011001100110000110011 0011001111001100110011000011001100110011110011001100110000110011 0011001111001100110011000011001100110011110011001100110000110011
The patterns present within this key are easier to discern if we represent it in a graphical form, by using white squares to represent zeros and black squares to represent ones:
The graphical key makes it easy to see that each of the nine dimensions has its own distinct and consistent pattern of ones and zeros. This can be made even more clear by drawing each dimension separately and arranging the number blocks in a circle.
Each circle is divided into 8 concentric circular rows, and each row into 32 segments. The segments are colored starting at the twelve o'clock position of the innermost row and continue moving clockwise and then outward until the circle is filled. The result is surprising and dramatic. Each dimension has a distinct style that is now clear to see:
The patterns revealed in each of these nine circles are intriguing. As mentioned above, each dimension has exactly 50% of its segments filled. The even dimensions can all be rotated by any multiple of 90 degrees without effect. This is not true for any of the odd dimensions. But the odd dimensions could all be made perfectly symmetrical if half their segments were inverted (the southern hemicycle in dimensions 1, 5 and 9, the western hemicycle in dimension 7, and the southwestern hemicycle in dimension 3). Dimensions 2 and 4 could be made more symmetrical if their inner 4 rows were inverted, but the same is not true for dimensions 6 and 8.
It's not yet clear what these observations really mean. The slightly muddled and interrelated symmetry of these circles conveys the same flavor I sensed in the starmaze from the first moment I encountered it. I still can't quite grasp the essential arrangement of the 2304 directed edges in the starmaze in the same way I can intuitively understand a square or a triangle. But these puzzle keys, and the dimensional circles they reveal, take me one step closer.
An even greater value of these keys is that they provide a framework for studying other hypercube puzzles. Seeing the starmaze in this wider context is quite enlightening.
Just as cube 1619 was one of 4096 possible order 3 puzzles, so the starmaze is one of 22304 possible order 9 puzzles. 22304 is about 10693, an almost unimaginably large number. So it is not even remotely possible to do a survey of all the order 9 puzzles.
It is possible, though, to study randomly-generated keys and get a feeling for which properties of a typical order 9 puzzle are common and which are rare. It is also possible to construct and study other specific keys and even spend some time wandering through the mazes generated by these keys.
I first began to understand coverage by studying the coverage rates of randomly-generated keys. I created a hundred random keys and calculated the coverage of each. My naive assumption going in was that I would see a wide spread in a bell curve centered on 50%. Instead all the coverage values fell in a narrow band between 60% and 67%.
As we saw in our survey of order 3 coverages, this has something to do with the dependencies between adjacent patterns. And the reason the values fall into such a narrow range probably has something to do with the law of large numbers. I generated random patterns by essentially flipping a coin 2304 times. As a result, the number of 0s and 1s in the key always came out about even, which is probably why all the coverage values came out about the same.
When I loaded the dice so that there was only about a 10% chance of getting a 0, the coverage increased, varying between 73% and 83%. The closer I got to all ones or all zeros, the closer the coverage got to 100%, with full coverage occurring even before reaching the neutral key due to the benign mutation effect described above.
Another set of keys I was eager to create was the rare set of minimum coverage keys. These puzzles fluctuate between two patterns, one which appears in its origin (and all other even corners) and the other, its inverse, which appears in all the odd corners. It was not at all obvious at first how to create such keys, but the study of the eight order 3 minimum coverage cubes discussed above provided the necessary clues.
As expected, the total number of minimum coverage hypercubes for any order n is 2n.
So of the nearly infinite number of order 9 keys, only 512
have minimum coverage, with origin patterns distributed like a 9-bit binary number.
The distribution patterns of any n-bit binary number can be found by consulting row n (in this case row 9)
of Pascal's Triangle. The 1s on either end tell us that
two of the 512 keys produce zero-cycle source/sink hypercubes (as was the case in 3 dimensions). In 3 dimensions we saw that
all of the remaining cubes produced the maximum number of cycles. But this is not the case in dimensions greater than 3.
Only 252 (126 + 126) produce puzzles with the 4 or 5 open cells in each pattern needed in a 9 cube for
the maximum of value of 20 cycles per room (2560 cycles altogether). One of these 252 is the "cross and corners" puzzle described
in Cycles and Seasons. Of the remaining minimum coverage keys, 18 (9 + 9) have
an origin with either 1 or 8 open cells (8 cycles per room), 72 (36 + 36) have either 2 or 7 open cells (14 cycles per room),
and 168 (84 + 84) have either 3 or 6 open cells (18 cycles per room).
This still leaves the problem of how to find the actual key values needed to generate these special puzzles. In 3 dimensions we saw that the 12-digit keys consisted of triplets with all eight possible combinations of two 4-digit sub-strings: 0110 and 1001. What we need in 9 dimensions, then, is all 512 possible ways of combining 9 sets of two 256-digit sub-strings. To find these sub-strings, we need to understand what's so special about 0110 and 1001.
0110, I discovered, is an example of what I call a "minimum coverage sequence". It turns out that this sequence is known to mathematicians as a "Thue-Morse sequence" and is used to generate fractal music. A minimum coverage sequence for a key of dimension d is produced as follows.
- Start with a seed value, either "0" or "1". This is your initial sequence.
- Concatenate the inverse of the sequence to the end of the sequence.
- Repeat step 2 a total of (d-1) times.
0
01
0110
01101001
0110100110010110
etc.
And a seed value of 1 produces the inverse sequences:
1
10
1001
10010110
1001011001101001
etc.
As you can see, the third rows above provide the two sequences we needed to produce our order 3 minimum coverage cubes. By simply repeating this process, we soon find the two 256-digit sequences we need to construct our order 9 minimum coverage hypercubes. I used this technique to generate and study three different examples, a "Sources and Sinks" key, a "Corners and Cross" key, and another typical minimum coverage key.
In order to study all these various keys, I wrote a HyperCard stack that allows me to quickly add a card for any particular key, immediately calculate its coverage and total cycles, and then interact with a working model of the puzzle produced by that key. A card containing the starmaze key has a nine-button display console that behaves just like the starmaze puzzle. Any other key will produce a different puzzle that has the same nine empty or filled circles and squares, but behaves in a different way. After all these years studying one hypercube puzzle, it was exciting to play with new puzzles, and gratifying to have my predictions verified.
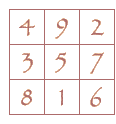The behavior of each puzzle can be defined by what happens when each of the nine cells are chosen. The cell chosen
always flips (this is a property of all hypercube puzzles), but what happens to the other cells vary.
When describing which cells are flipped, I use the standard starmaze cell numbering scheme
which is based on the Lo Shu (shown at right).
In neutral key puzzles nothing else happens - patterns shift one cell at a time. In minimum coverage key puzzles, each cell flips all the other cells, thus inverting the entire pattern. The other keys fall somewhere in between, with a given cell flipping a certain subset of other cells.
In keys with a rigid symmetrical pattern, like the starmaze, this behavior is completely consistent across all possible patterns, creating the perception of a fixed set of "rules". In less ordered, randomly-generated keys, the behavior is inconsistent and seems unpredictable - the more random the key, the more unpredictable the behavior.
Following is a set of 16 different experiments. For each key I provide the key itself, its coverage, the number of cycles it has, it's initial origin pattern, and its behavior. By studying these different examples, you can start to get a feeling for how the different puzzles behave and how the key determines that behavior. The keys are arranged in order of coverage from full to minimum.
The puzzle that started it all. |
Starmaze Coverage: 512 (100%) Cycles: 512 (20%)
| ||||
One of the 512 possible neutral keys. This is just like the all-zeros neutral key but with source/sink poles reversed. |
All Ones Coverage: 512 (100%) Cycles: 0 (0%)
| ||||
A neutral key with 29 random mutations far enough apart for full coverage. Usually the cells only flip themselves off, but will occasionally also flip another cell. |
99% Zeros Coverage: 512 (100%) Cycles: 0 (0%)
| ||||
Odd bars also had full coverage but the inverse "cross" origin (341). The 512 bar patterns are all variations of the neutral key, which can be seen as "all white bars". |
Even Bars Coverage: 512 (100%) Cycles: 0 (0%)
| ||||
50 samples varied in coverage from 73% to 83%. Behavior was entirely unpredictable. Origin occasionally varied. |
90% Ones Coverage: 395 (77%) Cycles: 95 (4%)
| ||||
100 samples varied in coverage from 60% to 67%. Behavior was entirely unpredictable. Origin changed with each sample. |
50% Ones Coverage: 318 (62%) Cycles: 537 (21%)
| ||||
Includes only the 256 patterns in which cells 1 and 2 are both open or both closed. Ones and zeros had same behavior but an inverse origin (511). |
Zeros and Ones Coverage: 256 (50%) Cycles: 0 (0%)
| ||||
Includes only those patterns in which cells 3 and 4 are in different states. All 128 cycles occur with cells 3 and 4 only. |
Checkers Coverage: 256 (50%) Cycles: 128 (5%)
| ||||
A cross between 50% random and "01101001" below. Origin changed with each sample. Coverage varied from 37% to 41%, cycles from 32% to 39%. |
0110 or 1001 Coverage: 200 (39%) Cycles: 952 (37%)
| ||||
Produced by alternating 64 01s with 64 10s. Cycles occur only with cells 1 and 8 and only from patterns, reached through cell 2, in which cells 1 and 8 are in different states. | Gray Coverage: 128 (25%) Cycles: 64 (2%)
| ||||
Dimensions reversed: 1 with 9, 2 with 8, etc. The same cells are flipped (evens twice, odds three times, 5 four times) but in a wierd yet symmetric fashion. |
Backward Starmaze Coverage: 128 (25%) Cycles: 192 (8%)
| ||||
Approaching minimum coverage using first 8 digits of minimum coverage sequence. 16 digits cuts coverage to 6%, 32 digits to 3%, etc. |
Repeat "01101001" Coverage: 64 (12%) Cycles: 0 (0%)
| ||||
Uses an altered minimum coverage sequence generated from '00' instead of '0'. Includes only 4 patterns: all open, all but cell 1 open, all closed, all but cell 1 closed. |
Stretched Minimum Coverage: 4 (1%) Cycles: 0 (0%)
| ||||
256 sources leading to 256 sinks. |
Sources and Sinks Coverage: 2 (0.4%) Cycles: 0 (0%)
| ||||
The maximum cycles puzzle described in Cycles and Seasons with 20 rings per room. Includes only 2 patterns: cross (341) and corners (170). |
Cross and Corners Coverage: 2 (0.4%) Cycles: 2560 (100%)
| ||||
Another of the 512 minimum coverage patterns with only 18 rings per room instead of 20. Dimensions 1, 2, and 8 are subtly different than the Sources and Sinks key. |
Minimum 131 Coverage: 2 (0.4%) Cycles: 2304 (90%)
|
Research into this area is ongoing. I have yet to achieve a sufficient mastery to easily generate a key for a given behavior or deduce behavior just by looking at the key itself. As this work continues, I will return to and expand this page.