This page follows the evolution of our efforts to create the basic map of continents and oceans. The next page focuses on the separate problem of "smoothing", creating realistic coastlines. Paul was eventually able to produce a program that produced large color maps, but there were many technical difficulties along the way. We may as well start with the algorithm itself. This is the way I first described it to a small circle of friends in 1989:

As all of you should know by now, Paul and I are working on our very own strategic war game. The first step in this process is to find a way to create randomly generated planets, complete with continents, islands, lakes, rivers, fiords, peninsulas, etc. We want to create maps that are interesting to play on, easy to make, and "natural looking".

There are all sorts of radicaly different ways to make a continent. One approach is to randomly spatter ovals of different sizes all over the map and then tidy up the edges so that they look more "coast-like". In trying this approach I discovered that vertical globs (made of ovals which are taller than they are wide) look much more natural than horizontal globs. On our planet we have lots of globs like Florida and India that stick down, but not many globs that stick out. Why is that, do you think?

Another approach would be to start with some kind of proto-continent and then split it up along random fault lines and let the pieces drift for awhile. This idea struck me as easy to visualize but difficult to implement, so I let it go.

My favorite approach so far is extremely simple. I start with 20 individual dots of land (I call them sparks) scattered at random. I put those 20 locations on the "spark list" and I then begin pulling items off the list at random and applying the following simple rule:

If the spark I've chosen is a land spark, I look at the eight cells adjacent to the spark's location. I mark each unassigned cell as either a land or a sea spark and add it to the spark list. To decide between land or sea I simply role the dice, with about an 80% chance of choosing land. But if the spark I've chosen is a sea spark, then ALL unassigned neighboring positions become sea sparks.

At first there is nothing but land. Every now and then a bit of water appears. But since water, in effect, grows faster than land, eventually each glob of land becomes surrounded by ocean and the ocean spreads until it fills 70% or so of the planet. The continents and islands produced are fairly interesting, albeit a bit too "raggedy". They have swamps, lakes, rivers, and convoluted coastlines. The algorithm still needs refinement, but I think it is quite promising.

paul1993-09-07:

So how big does the SparkList get? It turns out that when I wrote the initial code, years ago, I just sized it to maxRows * maxCols: 100 * 80 = 8000. This was stupid then; it's stupid and maybe "impossible" now. Why? Assume we smooth borders at 7x7 resolution. Assume also that 10% of the world is border. This is a wild guess, but it will have to do till someone does some calculations. Then the new SparkList size will have to be 8000/10 * 49 = ~40,000. Yow! We can't afford to be so sloppy any more.

I spent 5 minutes this afternoon thinking about the problem, and came up with a size estimate of ~1/15 the above. Needless to say, this is a vast improvement, if it's correct.

What do you think? Put your "Chief Algorithmist" cap on, and tell me how large I need to size the SparkList.

john1993-09-07:

A VERY interesting little puzzle. I shall, as you suggest, put on my "Chief Algorithmist" cap and see if I can come up with a better alogorithm, or at least a clearer understanding of the one we have.

Meantime, I did a quick bit of research and found the following quotation from the Mr. Wizard card which launched the continent grower way back in volume 11:

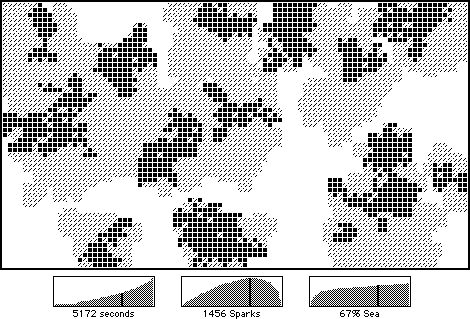
"The second graph shows the size of the 'Spark List'. Under the current arrangement this value rises and then falls. After awhile many sparks on the list don't need to be examined, because all their neighbors have already been assigned. This is one of the reasons the algorithm slows down; with a little more thought I may be able to reduce the wasted computations."

With some difficulty I managed to unearth my copy of the Continent Grower stack and examined this spark usage graph. This version generated a map of 53 by 93 pixels for a total area of just under 5000 square pixels. The sparkcount slowly rose to a maximum value of 1456 (about 30%) and then swiftly dropped back down to zero. I seem to recall that all the maps I generated showed the same basic pattern.

I will keep thinking about this. It would be helpful, though, if you could provide me with a plain English version of the current algorithm as you define it. That would get me up to speed and give us a common point of reference.

paul1993-09-08:

You want a plain English version of the current algorithm? I thought I supplied that last time. Well, I'll try again:

Set every cell in the world map to UNASSIGNED
Empty the SparkList
Randomly assign some points as land
     Mark them as LAND on the world map
     Add their map coordinates to the SparkList

Repeat until the SparkList is empty:
     Pick a random element from the SparkList
     Check its eight adjacent neighbors on the world map in turn
     (there will be fewer than eight neighbors if we're on a map edge)
     If UNASSIGNED:
          Mark the neighbor as LAND or SEA on the world map
          Add the neighbor's map coordinates to the SparkList
     Remove the old spark from the SparkList

That's it!

john1993-11-24:

When I first saw your red sparks I thought they were cities. And then I thought, why not make them cities? We haven't given much thought yet to selecting cities; the simplest method would be to use the initial sparks as cities (we would have to increase the number from 20 to what? 100?). On the other hand, this method would not ensure a proper balance between inland and port cities and between starting positions unless we did some additional fiddling. Just thinking aloud...

john1994-02-20

Now that I can quickly grasp the kind of worlds we are generating and what effects the sparkcount and land/sea ratio has on the big picture, I think we need to fiddle with some of our fudge factors. Our continents usually come out looking like bits of cat vomit splattered across a kitchen floor: too stringy, not beefy enough to earn the name "continent" (sorry, Ralph threw up this morning and the image is still fresh in my mind). The coastlines are OK, more or less, but we need more interior in the interiors. Perhaps firing globs instead of sparks will do the trick.

john1994-03-10:

Attached is a hypercard stack which allows you to compare our current continent generation algorithm with a new, modified version.

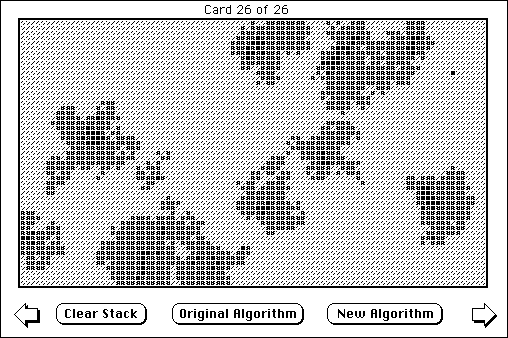
The stack takes about ten minutes to generate a 50 frame movie of the old algorithm and about five minutes to generate a 26 frame movie of the new algorithm. The stack includes extensive comments.

Basically, the new algorithm does two things: it provides for the creation of impassible mountains in continents, and it makes the continents much "beefier." I think both of these things are needed and, although the clump method has produced some improvement, I don't think clumps will ever completely solve the "stringy continent" problem.

The new algorithm is only slightly more complicated than the old. Basically, it divides growth into three phases. During the relatively brief first phase, land grows like water around the original mountain sparks. During the second phase no new mountains are produced and the sea begins to grow around the land. When about half of the positions have been assigned phase three kicks in: a simple cutoff in which all remaining unassigned positions are set to sea. This cutoff combats the tendency of the new beefy continents to grow together into a single world spanning super-continent and also cuts generation time in half.

This is my first cut at a modified algorithm, but it looks very promising. Let me know if you agree and how much trouble you would have implementing this method. The various fudge factors will need some adjustment; I'll keep working on the problem.

Incidentally, one interesting phenomenon that arises under the new method is the occassional appearance of a mountainous atoll, a single mountainous spark island. Since engineers are the only piece which can set foot on a mountain, they are the only piece that could disembark on such a rock (from a transport only). Once there, however, they could contruct a radar installation, upon which other pieces, including the helicopter, could then land and occupy. Kinda cool.

paul1995-12-28:

I'd like to request that the Alexander algorithmist put his thinking cap on and consider an adjustment or clarification to the world generation algorithm. The part that bothers me is the allocation of the temporary sparklist array. A quick review of the use of the sparklist (this is from 1+ year old memory, and may be a bit faulty):

The list gets "seeded" with a few random sparks.

Loop until the sparklist is empty: A random spark is removed from the list and its nearest eight neighbors on the map get inspected. If unassigned, they are assigned and added to the sparklist.

So how big does the sparklist get? No larger than the number of cells in the world, I guess, but that's a pretty big number (we looked at this briefly a few years back, but didn't come up with anything definite). The sparklist is actually a structure containing (x,y) pairs, so there are two integers per entry. One could also redundantly store the terrain type here, but I chose to not do this - my algorithm takes the (x,y) pair and looks up the terrain type on the world map.

If we store the (x,y) coordinates as 2-byte integer pairs (which seems reasonable to me), I'm confident the sparklist will never exceed rows x columns x 2 x 2 bytes. For a 100x100 world (not huge), this is 40,000 bytes - a pretty big chunk of memory. Or is it? Maybe I'm being stingy and old-fashioned here. On the Mac, I made the arbitrary assumption that the sparklist never exceeded a third or so of this size. This was necessary at the time because of an annoying 32K limit on data segment sizes on the 68K processor (or so I now recall). But once in a while this assumption was wrong, and all hell would break loose when I wandered past the end of the array. I guess I could put error checking in, and just quietly restart the algorithm from scratch on the occasions that the sparklist filled up, but error checking is a little expensive in a tight loop like this, and I'd rather deal with something slightly more deterministic.

So the challenge, I think, is this: either show a reasonable upper limit on the sparklist size, or switch to a new data structure that doesn't require random access.

A few words on the latter option: Needing to know an upper limit on size would go away if I could dynamically allocate memory for the sparklist. In my mind, this might be the preferrable solution. For a while I considered implementing the sparklist as a linked list. This solves the size problem, but creates another - random access into linked lists is unbearably slow. I'm sure this would ruin performance. But maybe random access isn't that important. What would happen if, in the original algorithm (above), we substituted "The last spark is removed from the list" for "A random spark is removed from the list?" Maybe we'd still get a nice random-looking world.

john1996-01-05:

Hmmm. There is probably *some* kind of upper bound other than the total number of cells in the map. I will indeed put on my thinking cap, if I can ever find it again (I seem to have misplaced it about a year ago). Your final suggestion about pulling any spark instead of the final spark seems OK to me - I don't believe that it matters and it's certainly easy enough to test.

I have become more convinced than ever that we need to assign an elevation to each cell. This could either be done by a minor modification to the existing algorithm (early sparks are high, later sparks are low) or by scrapping the algorithm altogether and using a more traditional fractal approach (which I don't know how to do at this point).

john1996-12-05:

An After Dark screensaver called Vista generates 3D continents on the fly (tropical, desert, or arctic) and flies over them occassionally diving and turning at a reasonable speed. You can see reflections of clouds skittering across the laketops as you barrel-roll across.

Gee, wouldn't it be nice if we could fly like this in Conquest? Better yet, as we occupy land it could turn green and lush, while the enemy's land turns Mordor-brown and pitted with craters. Our sim cities could sparkle while theirs rust and decay.

Just a thought...

paul1997-02-12:

What continent does a city reside in? Here's one simple solution to the dilemma: Each land spark (or clump) is given an ID. As the world is generated, this ID is propagated to each offspring land cell.

Upsides:

• It's simple.
• It's quick.

• It consumes memory - 1 byte/cell worst case; 1 bit/cell best case.
• This doesn't address the problem of naming oceans.
• Two or more sparks may generate a single continent ("Eurasia"). How confusing will this be?

I think having a 1 byte/cell tag may well be worth the memory hit. I still have vague fantasies about an object oriented approach where pieces and cities reside in continent containers and inherit attributes or receive messages based in part on what continent they reside in. Such location tags may prove indispensible for implementing stuff like that. (I think you would need *at least* 6 bits to allow for a 64 island archipelago; probably a full 8-bit byte makes the most sense.)

I do think, though, that every speck of land on the same continuous land mass (Eurasia) should wind up with the same ID tag. As proto-clumps collide, a table could be created showing which proto-ID tags now reside on the same land mass. You could then either A) make an additional pass through the finished cells updating continent ID tags, or B) keep the original tags in place but always filter them through the table in a way that was transparent to the user:

   A) contID(x,y) = tag(x,y)

   B) contID(x,y) = lookupTable(tag(x,y))

Will players ever be able to divide continents by constructing a Panama Canal or even establishing an arbitrary 42nd parallel-style demarcation line? If so, option A would be preferred bacause in such cases continent ID would no longer flow directly from proto-clump ID.

I also think we may eventually want some additional information attached to each cell. Maybe 2 or 3 bits could be set aside for an openland / mountain / forest / swamp / river / road kind of identifier. If we ever get into *serious* continent rendering, we may want elevation data as well (which could arise naturally from our existing generation algorithm). It's conceivable that political boundaries might come into play someday (color-coded territories within continents).

As for the oceans, I wouldn't worry about that just yet. It's not clear that there's any reasonable way of dividing a continuous ocean (other than just whacking it up along longitude lines) or any compelling reason to care.

paul1997-02-20:

Thinking about the world generation algorithm...

You'll recall that in prior versions of the algorithm, we start with an array of sparklist locations and remove elements randomly as the world is generated, replacing them in the array with any of their nearest neighbors that get assigned during that pass. The problem with this scheme is that we need to pre-allocate a large array of worst-case size.

So one of us (me?) proposed switching to a stack. The idea is that you always pull the top element off the stack, then push on any of the six nearest neighbors that get assigned that pass. If the stack can grow dynamically, this nicely avoids wasted space. But it occurred to me this morning that it probably doesn't work. Chances are the first spark will grow for a while, then at least most of the rest of the world will fill up with sea before the stack empties enough to get to even the second spark. If you start with ten sparks, I bet six or eight will wind up totally surrounded by land or water before they get a crack at growing. This is not a good thing.

What's the solution? I'm betting that a queue will solve the problem.

Imagine we start with ten sparks. The first one will be pulled off the queue, and its eight nearest neighbors will be assigned and pushed onto the end of the queue. Then the second spark will get its turn to grow, and its children will be pushed onto the end of the queue. Then the third spark, and so on, until all ten sparks have had a crack at growing. At this point, you're back to servicing whatever the first spark left behind, and so on again, until the world is entirely mapped out.

My biggest concern is that this may generate too-uniform growth; maybe the random selection of the array-based algorithm is important to the final look of the world. To help combat that, I plan to randomly vary initial spark sizes from 1 cell to some requested upper limit. But I guess we just won't know how well this algorithm will work until we generate a bunch of worlds.

On this last subject - if I send you a file of 1's and 0's to represent land and water, how difficult is it for you to turn this into a blue and green world map - a pict or gif or whatever? I'm no sure if there will be an easy way for me to do the display myself from C++, so telling if my program is doing the right thing may be problematical.

john1997-02-20

It's been a frantic day here, so I've only had a few seconds to read over your note. My initial reaction is that I am skeptical about all of the variations you propose because I *think* the behavior of choosing from the spark list at random is the very essence of the algorithm - muck with that and all bets are off. The stack proposal, I think, would result in the first spark growing like a cancer; the second spark would not be touched until the first was fully contained. The queue proposal is better but might result in more uniform growth since each spark would expand outward in a uniform way like ripples in a pond and the interference between ripples would proceed in a relatively uniform manner. I can't predict with confidence what would happen under both models, and agree it would be interesting to try them and see.

Once upon a time I did have a Hypercard stack which would plot a file of 1s and 0s (or was it 1s and 2s?) - chances are good that I can find it. I can then take a screenshot, pop it into Photoshop, and let the colors fly! I will be glad to email you a BMP (or whatever you require).

paul1997-03-16:

Attached is a typical world generated using the queue-based variation of our standard algorithm. The result is land masses which have a curious diagonal stringiness - not at all what we want. The cause of this seems evident, so now I'm off to attempt a quick fix.

paul1997-03-17a:

My hunch was that the problem was mostly due to the fact that I process cells in a fixed order. A little background, in case you're rusty on the details. For each spark, I look at each of the eight nearest neighbors to see if they've been assigned, and if not, I assign them and add them to the (stack, queue, or array) structure of cells to check later. With the queue-based algorithm - well, actually, with all of the algorithms - I place them in the data structure in a fixed order. If "5" represents the center cell, then using the following numbering

123
456
789

the cells are always added in the following order: 12346789. With the queue, then, they always get pulled off in the same order, and I'd expect to see a diagonal stringiness.

My attempted fix yesterday was to randomize the order the neighboring cells go onto the queue. Surprisingly, I didn't detect much of a difference in the generated worlds. It's quite possible there's some other bug in my code which is exacerbating this problem, or maybe the queue data structure is just fundamentally wrong for this algorithm. For completeness, and since you say it's so easy to crank out the GIF files, I enclose a sample world using this modified algorithm. Note that I no longer bother to print out "W" for water (or was it "S" for sea?). You'll only see "L" for land. Later (i.e., tonight or tomorrow) I may also add something like "C" for city.

The good news, such as it is, is that the algorithm is plenty quick. A world of this size (50 x 70) takes maybe a second to generate. A 300 x 300 world takes 5 seconds, and 500 x 500 is about 10 seconds. Of course this is on a 200 MHz Pentium Pro processor, but it's running through the debugger with all optimizations turned off. Later I'll check on non-debugger fully optimized speeds, just for grins.

paul1997-03-17b:

Abandoning the queue saves lots of time - logical, because my queue algorithm is allocating memory each time a new element is added, whereas my "dynamic array" algorithm allocates enough for the entire array in one statement. Anyway, a 300x300 world takes maybe a second with the array vs. 5 seconds with the queue, both in the debugger with optimizations disabled. For grins, I cranked the array algorithm up to a 1000x1000 cell world with 1500 starting sparks. Debug/No optimizations took 30 seconds - pretty impressive, in my book (of course I realize that the time consuming operations, like smoothing, are yet to come). No debug/optimize for speed took 20 seconds.

My guess is that with Strategic Conquest rules, it would take months to play a game with a map of this size if opponents are evenly matched. I was about to say that we can now generate worlds larger than we'll ever want - but who knows? Maybe when we start our first 100 - player game on the Internet, much larger worlds will be desirable ;-)

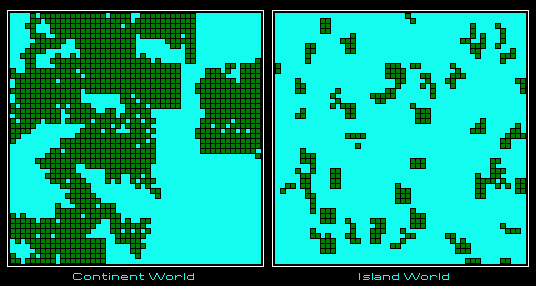
paul1997-03-18c:

OK, if you have time, here are two more maps to generate. The idea here is to show a little of the power of the parameters (size, land probability, etc.). These maps show two ends of the spectrum. IslandWorld was generated using 50 seeds of up to 3 x 3 in size with a land probability of 0.25. ContinentWorld was generated using 10 seeds of up to 10x10 in size with a land probability of 0.9.

john1997-03-28:

As for all that excess Alexander energy I would propose nailing down the continent IDs while the code is still fresh in your mind and then adding cities.

Mountains and Rivers are next on my list, but I'm not sure how best to generate them. Seems to me we took a stab once at mountains by correlating the elevation of a pixel to its order of creation (the first pixels are the highest, first 10% or so marked as mountains). I have no idea about rivers, but there are many possibilities. Are you seeing many inland seas/lakes/ponds? If so you could use elevation to calculate shortest path drainages. Or you could just pick a random spot on the coast and drill inward for a random length.

Minor idea: show river cells as either narrow or wide; some ships could travel up narrow rivers, others (battleships, carriers) could only navigate wide rivers.

paul1997-03-31:

I had a minor sinking feeling when I first saw your message and realized I wasn't sure how to consolidate countries into continents. Then I thought "Hah! Here's a good use for a stack. I'll just go methodically around the world, and whenever I find a land cell without a parent continent I'll assign it to a new continent and push its land neighbors onto the stack for subsequent assignment." Just like the initial land growth phase, only a little different. For one thing, there's no need for the random element - so a stack should work fine. But when I started the coding, I realized there's a simpler solution yet - recursion.

Here's the modified algorithm:

Walk the entire array of cells. Each time you find a land cell that isn't assigned a continent, bump up the continent count and assign that cell. Also check its eight nearest neighbors. Any that are land are guaranteed to be continent-unassigned, so assign them to the continent just identified, and call the eight-nearest-neighbors-check routine recursively on each of the land neighbors in turn.

Note: the algorithm happens in a pass after all land generation has occurred. The former "continent" identification is now renamed "country," and is otherwise unchanged.

OK, I know this algorithm is doubly inefficient:

1. Recursion overhead.
2. Most land cells will be visited multiple times. Once, guaranteed, walking the entire array of cells in the outer loop. One or more additional times as neighbors of other land cells.

Here are the first two 75 x 75 worlds with continent assignments.

It looks like I have the land probability factor set a little high for ordinary worlds, but the results are pretty interesting nonetheless.

We did have mountains implemented at one point. All sparks were considered mountains, and I think there was a special "mountain probability" variable that decided if more mountains were generated, possibly much as you broadly outline below. I don't remember the details any more.

I was considering implementing your suggestion of recent weeks to use country boundaries to identify streams. Now, though, I wonder if we shouldn't use the boundaries for roads or ridge tops or something else. Most of your proposed enhancements (rivers, river widths, elevations) will be kind of tough for me to deal with until I improve the resolution and actually display world maps. Of course this will likely cut you out of the loop unless you get a PC, or I figure out how to generate .bmp files. Maybe it's time to worry about cities now. Any thoughts on how we should place them? And what else can we focus on before I need to worry about actual display code?

john1997-04-08:

It has long been my suspicion that fractals are the way to go, but like you I have only a vague idea how to go about it. On the tape (which you should receive by Thursday) I rambled briefly about adding a 3rd dimension to our current algorithm by allowing sparks (seeds?) to grow slighly up and down as well as within a plane.

In the meantime, I'll keep an eye out for good fractal books. Happy packing!

john1997-04-09:

As for cities, haven't given it much thought. I surmise that Conquest's algortihm is not entirely random. It seems that two cities *never* appear directly adjacent to each other. Should we have such a restriction? Actually, I think a naturally occuring twin-cities metropolis would be an interesting wrinkle.

I believe Conquest also ensures that opponent starting positions are approximately comparable - that is, both starting islands usualy seem to have the same number of cities and are guaranted to have at least one port city (else how would you ever get off your home island).

One strategy is to scatter them at random somehow and then make a second pass to correct any anomolies (but if we allow adjacent cities and edge-of-the-world cities that might not be necessary). We could either scatter the cities totally at random, or continent by continent according to some randomized quota. Another variation is to ensure parity between hemispheres by alotting the same number of cities per quadrant.