Smoothing proved to be a daunting challenge. We were aware of the then new technique of fractals, but began by first experimenting with an ingenious extension of our existing continent algorithm - basically establishing an exact "proto-shoreline" and then growing micro-continents inside it. Part one of this page describes the initial concept. Part two is an early word document I created to describe exactly how to find this proto-shoreline. Part three reveals some of the details which had to be worked through. Part four shows the two maps we were able to produce.

The Concept

I have come up with a rather elegant approach that MIGHT solve our smoothing problem. Basically the idea is to first generate the map in the usual way and then:

1. Go back and identify the "shoreline zone", all coordinates that are either land adjacent to sea or sea adjacent to land.
2. Delete all shoreline zone assignments and consider the new blank space AT TEN TIMES THE RESOLUTION as a new world. That is, each deleted coordinate is now treated as a ten by ten block of unassigned micro-coordinates.
3. Insert one land micro-spark adjacent to the inland for each deleted land coordinate.
4. Apply the standard growing algorithm to that set of sparks until the entire unassigned coastal space is filled!

This note generated an exchange in which Paul and I worked out what might be involved in implementing this idea. john1992-07-13 includes a lengthy question and answer section about the algorithm. A year later, in paul1993-09-08, Paul works through "one-pass smoothing" with some text-based diagrams. But in paul1993-09-11, he leans toward two-pass smoothing and expresses some concern about the memory and processing requirements. The problem of precisely identifying the shoreline was still not entirely nailed down. In john1993-10-31 I included a word document which dealt with this.

Finding the Shoreline

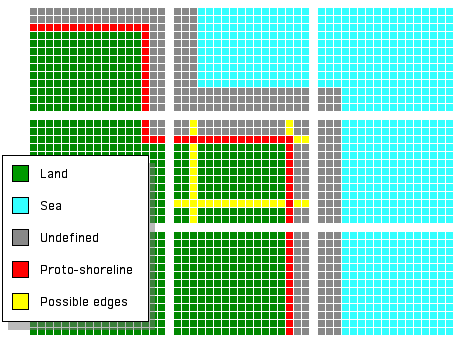
The pixels shown in red comprise the proto-shoreline in this example. For each land coordinate, the undefined pixels are those from the edge of the coordinate up to but not including the proto-shoreline. For each sea coordinate, the undefined pixels are those from the edge of the coordinate up to and including the "continental shelfline," a line determined in exactly the same way as the proto-shoreline. The problem, then, reduces to finding the proto-shoreline.

The proto-shoreline pixels of any coordinate will be found along the set of possible edges (shown in yellow). These edges consist of four "major edges" which form the boundary of an inner square, and eight "minor edges" which extend perpendicularly from each of the four corners of the inner square. In the example above the proto-shoreline for the central coordinate (C) consists of the north and east major edges (N, E), the south by southeast minor edge (sse), and the west by northwest minor edge (wnw). The coordinate to the west of the central coordinate (Cw) includes only two minor edges in its proto-shoreline, the north by northeast minor edge and the east by northeast minor edge (nne, ene).

Choosing from among these edges is not as simple as it might seem. There are 256 different ways in which a land coordinate can be surrounded by land and/or sea coordinates. Fortunately, each of the twelve possible edges can be included (or not) on the basis of a simple test.

The notation is as follows. The four major edges are represented as uppercase letters (N, S, E, and W) and the minor edges by lowercase letters (wnw, nnw, nne, ene, ese, sse, ssw, and wsw). The coordinate in question is represented by a capital C, and its neighboring coordinates are expressed using subscripts; thus C_n is the coordinate to the north, C_w is the coordinate to the west, and C_nw is the coordinate to the northwest. The following table provides expressions to determine if each of the twelve edges of a coordinate C should be included in C's proto-shoreline (or continental shoreline).

Edge	If And Only If
N	C ≠ Cn
S	C ≠ Cs
E	C ≠ Ce
W	C ≠ Cw
wnw	C = Cw AND NOT (C = Cw = Cnw = Cn)
nnw	C = Cn AND NOT (C = Cw = Cnw = Cn)
nne	C = Cn AND NOT (C = Cn = Cne = Ce)
ene	C = Ce AND NOT (C = Cn = Cne = Ce)
ese	C = Ce AND NOT (C = Ce = Cse = Cs)
sse	C = Cs AND NOT (C = Ce = Cse = Cs)
ssw	C = Cs AND NOT (C = Cs = Csw = Cw)
wsw	C = Cw AND NOT (C = Cs = Csw = Cw)

Essentially, a major edge is included in the proto-shoreline if the type of coordinate (land or sea) is the opposite of that of the neighboring coordinate in the direction of that edge. A minor edge is included if the element of the coordinate matches the neighboring coordinate in the direction of that edge unless all four of the nearby coordinates match. Once these edges are assigned it easy to form the initial land spark list and determine which pixels are part of the shoreline area. Applying the same continent generation algorithm on a pixel scale then completes the shoreline.

Devil in the Details

I have been grinding away on the smoothing algorithm and am beginning to see that a fair amount of experimentation will be required before we can work out all the details... I see two problems. The first is that the sparklist is large to the point of being unwieldy (although not as large as I had originally feared). The second is that the huge initial land-to-sea ratio may prevent sea pixels from forming in the shoreline area. At the macro level, with 20 initial land sparks, the land/sea ratio rises to about 50/50 within the first 500 sparks. Under my current smoothing approach, by the time the sparklist grows from 38000 to 50000, I would expect only about 2000 (or 4%) sea sparks. By the time the sea sparks start to achieve critical mass, all the shoreline area would already be landfill. That, at least, is my guess.

After a week or so, in john1993-11-13, I came up with three possible solutions.

The Full Map Approach
Cost: 2,520,000

The idea here is to use the display map as a lookup table. The full display consists of a 8 bit deep color window that is 1800 pixels wide and 1400 pixels high. To use this window as a lookup table you would first paint the pixels of the shoreline area a neutral gray. As the continent generation algorithm inspects the sparklist, it peeks at the actual color of the pixels to determine their state (land, sea, or not-yet-defined) and paints as it goes. This is the simplest approach but also the most costly (unless you are already storing this map in all its glory). Unfortunately, OracleCard does not let me use this approach. Do you store the whole map at once in your C program? Or do you summon it up on the fly as the user scrolls around?

The Seashore Blocks Approach
Cost: 750,000 + 20,000 for additonal index table

The second approach, and the one you seem to be gravitating towards from what I understand, is to store pixel details only for shoreline coordinates. Since about 30% of the coordinates in a typical map include shoreline pixels, this approach provides an immediate savings of 70%. However it does require some extra bookkeeping. How can the continent generation algorithm do a random x,y lookup when all the discontinuous coastline coordinates are smashed together into a single continuous mass?

The technique I used was to construct a separate shoreline map lookup table. This table has one element for each of the 10,000 coordinates of the macro-map. If the coordinate in question is inland or deepsea, the corresponding element is 0. If the coordinate is part of the shoreline area, the element is an index to the list of seashore coordinate blocks. The first seashore coordinate is assigned a 1, the second a 2, and so on up to the total number of seashore coordinates identified (about 3000). This map can be generated during the process of identifying the seashore pixels.

Given an absolute pixel location for a spark (say 1623,1230), the continent generation algorithm can lookup the current state of the eight neighboring pixels as follows. First divide by 18 horizontal and 14 vertical to obtain the macro coordinate in which this pixel is located: 91,88. Now lookup element 91,88 in the shoreline map and find the index number, say 2744. (No spark will ever have neighbors that fall within a non-seashore coordinate, so the index returned will never be 0; you still have to beware of pixels on the edge of the map, however.)

Now find coordinate pixel block number 2744 and calculate the local offset (1623-(91-1)*18,1230-(88-1)*14); in this case the offset is 3,12 and all 8 neighbors can be found in the same pixel block. When the pixel falls on the edge of a block you will need to return to the shoreline map to discover which block holds some of its neighboring pixels.

The Undiluted Pixels Approach
Cost: 300,000

Although the second approach does result in a 70% storage savings, it is still rather wasteful. It turns out that, on average, only about 40% of the pixels in a shoreline coordinate block are included in the original shoreline area; the remaining 60% is dead weight, which will never be examined or altered. The Undiluted Pixels Approach squeezes out the remaining fat but requires a different method to do the lookup. You will have to decide for yourself if the tradeoff is worthwhile. I was forced to partially implement this method.

The basic idea is to replace each sequence of non-shoreline pixels with a single value: the number of pixels in the sequence. For each of the 1400 rows of pixels in the full map, scan across and replace every set of n land/sea pixels with the number n. (If you wish to store this value as a single byte you can break it into multiple numbers which add up to n; 302 could be represented as a 255 followed by a 48).

The endpoints of each sequence are not included. Thus if a string of 115 sea pixels are followed by 6 undefined shoreline pixels, the line would be reduced to the number 114, followed by a '2' to represent the single ending sea spark, followed by 6 '0's to represent the six undefined pixels. 0 means undefined, 1 means land, 2 means sea, and 3 or higher means a sequence of length n. (A sequence of 2 non-shoreline pixels should be represented as either '11' or '22'). The shoreline space, then, is represented by 1400 strings of varying length (typically about 220 bytes).

The lookup procedure does not require the shoreline map needed by approach two; we are dealing entirely on the pixel level. To lookup a spark at <1623,1230> we first find string number 1230. Our problem is then to figure out which byte in the string corresponds to 1623. We determine this by starting at the beginning of the string and counting. A 0,1, or 2 byte adds 1 to our count; anything higher adds that value to our count. We keep counting until we reach 1623. The sparks we need to lookup are guaranteed never to fall within one of the reduced sequences; the byte corresponding to 1623 will be a 0, 1, or 2, never anything higher; neighboring pixels which fall within a reduced sequence have, by definition, already been assigned and thus are never altered or added to the sparklist.

To lookup all eight neighbors we will need to scan through 3 strings (e.g. pixels 1622-1624 in strings 1229-1231). For added efficiency we could start at the end of a string and count down from 1800 whenever the horizontal value is greater than 900; that way we never have to count past the center of a string. A little more effort is required constructing this 1400 string shoreline space map, but the lookup procedure may be somewhat easier to implement. I'm not sure what the speed cost would be in C; it might not be that bad.

As I mentioned, I was essentially forced into using a hybrid of aproaches two and three. I use the shoreline map from approach two to locate the appropriate coordinate block, but I reduce the block itself by stripping non-seashore pixels from the end of each of the 13 lines in the block (it's 13 and not 14 because I use the 14th line (and 18th column) to form gridlines on the display map). This provided me with an additional savings of about 30% which was just enough to greatly simplify my division into multiple containers.

One week later I achieved a breakthrough and, in john1993-11-19a, released the following jubilant announcement:

For General Release:

Coastal smoothing was achieved today, Friday November 19, 1993, at 1:29 PM Pacific Time at the west coast facilities of the Alexander Research Institute. Chief Algorithmist John Cartan could not be reached for comment; sources report that he is exhausted after "pulling an all-nighter." Early reports suggest that the algorithm is promising but definitely needs further refinement. The staff at A.R.I. is now transmitting screenshots to their Salt Lake City office for further analysis.

The Maps

The coastline produced is interesting, but flawed in several respects. The inward rushing of the sea was more vigourous than I had anticipated; as a result, the initial land sparks tend to form lacy arms that stick out from the rest of the coast. Much of the sea extends uninterrupted to the edge of the shoreline area so that many straight line segments and, even worse, intact 90° corners are visible. And when the land sparks do take hold, too often they push all the way to the edge, revealing more straight line segments. The overall effect is boxy and unnatural.

Although not yet acceptable, the technique certainly produces dramatic coastlines and I think, with some adjustment of the initial spark selection, can be much improved. My next experiment will be to return to my first instinct and select entire edges of land-based seashore coordinates.

The second map was better, but still not very smooth. From john1993-11-19d:

This time I allocated 14% of the initial shoreline space as starting land sparks (line segments along the edges of land-based shoreline coordinate blocks). The results are much better. This time, instead of occupying 59% of the shoreline area, the sea only rose to a level of 37%.

Although further fudge factor fiddling can improve the current coastline somewhat, it now seems clear that the micro-continent generation method will always produce a characteristic "lacy" look, a coastline that is not smooth but, rather, torn into powder. I'm not sure whether I like this look or not.

After further discussion, Paul and I both agreed that this brave attempt at creating smooth coastlines had failed. From john1993-11-21:

I also agree that the lacy coastline produced by my algorithm is "interesting but distracting." Given the massive time investment I made in order to finally taste the fruits of this approach I am disappointed but will bravely carry on in search of a better way.

Unfortunately, though, we were never able to find that better way. In the final days of our waning Alexander dialog, we agreed that fractals were the way to make realistic coastlines and vowed to learn more about them. Fractal-generated coastlines are now commonplace and would certainly be employed in any 21st century implementation of this sort of game.