
 From the moment I first encountered the puzzle that became the starmaze, I wondered what it would be like if each pattern was a room and each choice was a door. How would it feel to stand inside one of those rooms? What would I see behind each door?
From the moment I first encountered the puzzle that became the starmaze, I wondered what it would be like if each pattern was a room and each choice was a door. How would it feel to stand inside one of those rooms? What would I see behind each door?
Thirty years later, with the help of Google Sketchup, I am flying through the starmaze like a bird! I am swooping over towers and under bridges. I am plunging into tunnels, trudging up long staircases, and sliding into vast chambers that literally take my breath away. All the work I've done along the way, the Starmap, the Starmaze Explorer, the endless yellowpads filled with equations, has been my price of admission to this brave new world I call the 3D starmaze.
The most amazing thing is that, to a great extent, I am discovering these spaces, not inventing them. As a result, I am genuinely surprised when I step into a 3D starmaze room for the first time. Friends who have politely listened to my lectures on hypercubes, and who now see video fly-throughs of this suddenly tangible world, are surprised as well.
As I write this, the work to "excavate" the 3D starmaze is still ongoing, but I have come far enough to be able to document, in some detail, how it works, what it looks like, and how it relates to my original visualization of the maze, the starmap. I hope that this overview will help visitors understand how this enormous virtual monastery, with its towers and courtyards and bastions and underground caverns, is actually a direct mathematical realization of the starmaze puzzle, and that moving through this model provides insights (and surprises!) that would be hard to obtain in any other way.
About Dimensions
I often describe the starmaze as a 9D structure, so the fact that I have produced a 2D map (which is really 3D) and now a 3D model (which looks nothing like the map) may seem confusing. Those who furrow their brow at the very idea of a space with more than three dimensions become exasperated when I can't even seem to decide how many dimensions this thing actually has.The truth is that the starmaze does not "have" a particular number of dimensions. It is simply a set of 512 states combined with some rules that determine which states lead to which. A computer scientist might choose to represent those states as memory addresses. A mathematician might represent them as members of a set. An artist might represent them as points in space. Likewise, you could represent the rules as words in a computer language or numbers in an adjacency matrix or arrows in a cave painting.
Together, the states and rules comprise a system that could be represented as a state machine, a network, a permutation group, a directed graph, a highway map, a kinetic sculpture, a handheld puzzle, or even a monastery. It may seem strange that words, numbers, rotations, arrows, chutes, and ladders can be so interchangeable, but my study of the starmaze has helped me understand that a single system can be represented in many different ways.
If I am more often drawn to geometric representations it is only because I find that approach so fundamental. Algorithms and equations are just as valid - and just as beautiful in their way - but do not as easily evoke a sense of wonder in most people. An appreciation of space is something we are born with, something which comes before our words and numbers. Indeed, I think space is the deep well from which all language and mathematics are drawn.
The starmaze fits most naturally into a nine-dimensional space because the 512 states and the 2304 directed edges map perfectly to the corners and edges of a 9 dimensional hypercube. In 9-space the starmaze becomes a perfect crystal. Each corner becomes identical and equidistant from its neighbors. Each passage is perfectly straight and all are exactly the same length. Its many symmetries are laid bare.
Other spaces are possible, depending on exactly what aspects of the maze you want to represent. It would be just as valid to draw the starmaze in a space of 18 dimensions, or 512, or 2304. With 2304 dimensions you could plot every possible kind of 9D hypercube puzzle on the corners of a far vaster cube, sliding from puzzle to puzzle instead of room to room. Magnificent, but unwieldy.
Fewer dimensions are equally valid, though you can no longer use a purely binary space. If you allow each dimension to hold more than two possible values, then a space of 8, or 7, or even 3 dimensions is still plenty big enough to hold a mere 512 points. But each time you reduce the number from 9, you have to bend and twist the maze's edges, just as you must do when drawing a cube on a piece of paper. You can still have the correct number of edges departing each corner, but they can no longer be mutually perpendicular.
It is precisely this process of folding simple structures into ever smaller spaces that I find so interesting. It's a metaphor for any situation in which complexity arises naturally from simplicity. The starmaze structure is exactly the same in 3 dimensions as it is in 9 - it just seems more complicated. But if you look deeply enough into the tangled passageways you can still sense the simplicity implicit in the surface patterns, just as you can sometimes hear a children's song inside the movements of a great symphony. I think the universe has this same quality. Whenever we discover a new law of physics we are catching a glimpse of something very, very simple - the cosmos in our chaos.
But there is a limit to this process of folding. Although you can draw all the corners and edges on a piece of paper, as I did with the starmap, you cannot truly represent the maze in only 2 dimensions. This is because, strictly speaking, the edges are never supposed to intersect each other. Like the map of an interstate highway overpass, intersecting lines on a piece of paper are understood to represent roads or edges that, in actual fact, pass over or under each other. The 2-D starmap is like a woven rug: flat from a distance, but actually full of woven threads or "pipes" that could not be constructed without a third dimension. Mathematicians call this kind of graph "non-planar".
From Map to Maze
The starmap and the 3D maze, then, are two different but equally valid ways of folding a 9-dimensional cube into a seemingly more elaborate 3-dimensional structure. They look so different because they are designed for two very different purposes:- Rooms in the Starmap are arranged to reduce the number of explicit passages in order to make a flat map that is compact and easy to comprehend.
- Rooms in the 3D Starmaze are arranged to exploit all three dimensions in order to make a mental model that is realistic and easy to remember.
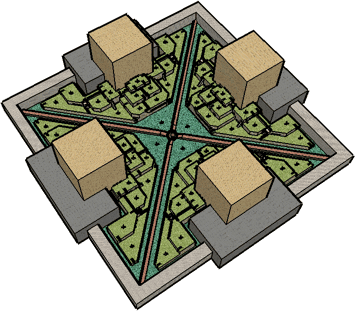
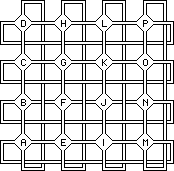 The diagram at right shows the layout of microcosms in the starmap.
There are a total of sixteen, labeled from A to P, each containing 32 patterns.
The microcosm is the most natural way of organizing the maze; it is formed by holding the
yin (corner) cells constant
and allowing the yang cells to vary.
Although it looks flat, if you study the connecting pipes you will see that overall structure
forms a torus. That is, the left edge is connected to the right, and the bottom edge is connected to the top.
If you joined the left and right edges to form a tube you could dramatically shorten the long horizontal pipes.
And if you then joined the two ends of the tube to form a torus, you would shorten the long vertical pipes as well.
The diagram at right shows the layout of microcosms in the starmap.
There are a total of sixteen, labeled from A to P, each containing 32 patterns.
The microcosm is the most natural way of organizing the maze; it is formed by holding the
yin (corner) cells constant
and allowing the yang cells to vary.
Although it looks flat, if you study the connecting pipes you will see that overall structure
forms a torus. That is, the left edge is connected to the right, and the bottom edge is connected to the top.
If you joined the left and right edges to form a tube you could dramatically shorten the long horizontal pipes.
And if you then joined the two ends of the tube to form a torus, you would shorten the long vertical pipes as well.
Actually, the grid of microcosms is really a flattened tesseract. But the 16 corners of a tesseract map nicely to evenly spaced points on the surface of a torus. A torus almost seems four-dimensional with its two-dimensional horizontal circles orthogonal to its two-dimensional vertical circles. But of course it's a completely three-dimensional object, as familiar as a donut. That's why it works so well as a scaffold for arranging microcosms in 3-space.
This is precisely what I did to form the basic structure of the 3D starmaze. A torus is slippery, though: it's harder to label and remember positions on a torus because it is so symmetrical; unlike a flat map it doesn't have obvious rows and columns and an unambiguous lower left corner to serve as an origin. So before I could have any hope of keeping things straight, I had to develop a memorable way of positioning and labeling the microcosms.
The basic idea was to assign each column in the original grid to a point on the compass: east, south, west, and north - arranged in that order to form a natural circle. To further cement the differences I associated each direction with a different landscape: east with a (green) forest, south with a (yellow) desert, west with a (blue) ocean, and north with snowy (white) mountains. I imagined the starmaze as sitting at the intersection of these landscapes, perched on a cliff at the edge of a western ocean, with mountains to the north, a desert to the south, and a vast forest to the east. (The fact that I happen to live in California may have subconsciously influenced me to make these assignments.)
To each row of the original microcosm grid I assigned a different structural shape: a massive rectangular "bastion", a tall square "tower", a triangular terraced "courtyard", and, beneath the surface, a zigarat-shaped "deep". I designed these shapes to contrast with one another and to fit together neatly into a pleasing, compact layout. By this time I had already begun thinking of them as "houses" rather than microcosms.
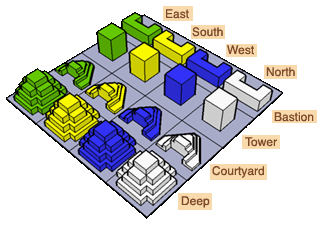 The resulting system is shown at right. Microcosm A becomes the East Deep and
Microcosm P becomes the North Bastion. Each type of structure now connects in horizontal
circles: the East Bastion leads to the South Bastion which leads to the West Bastion,
then to the North Bastion, and back to the East Bastion - and the same for the other types.
In addition to the four horizontal circles, there are four vertical circles at each of the four
points of the compass. The North Deep leads up and in to the North Courtyard, then further up to the
North Tower, then back down and out to the North Bastion, and finally back down to the North Deep.
I call the four different types of houses sharing the same compass direction a "temple".
The resulting system is shown at right. Microcosm A becomes the East Deep and
Microcosm P becomes the North Bastion. Each type of structure now connects in horizontal
circles: the East Bastion leads to the South Bastion which leads to the West Bastion,
then to the North Bastion, and back to the East Bastion - and the same for the other types.
In addition to the four horizontal circles, there are four vertical circles at each of the four
points of the compass. The North Deep leads up and in to the North Courtyard, then further up to the
North Tower, then back down and out to the North Bastion, and finally back down to the North Deep.
I call the four different types of houses sharing the same compass direction a "temple".
The entire structure can now be visualized in the following diagram:
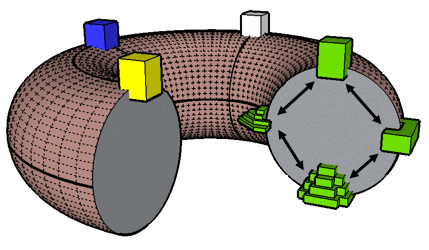
As you can see, the four towers are connected by a horizontal circle on the top of the torus. When the remaining houses are added, the four courtyards are connected by a circle on the inside, the four bastions by an outer circle, and the four deeps by a circle on the bottom of the torus. If you slice open the torus at any cardinal point you will see the vertical circle associated with that temple. Here the East (Forest) Temple is shown with the tower at top circling down to the outward facing bastion, then to the deep at the bottom, then up to the inward facing courtyard, and back again to the tower.
The torus is helpful in remembering how the sixteen houses relate to each other, but in order to construct a more compact, tightly connected structure I deflate the torus until the houses snap together. The different shapes fit like puzzle pieces to form a symmetetric, habitable structure that looks something like a monastery:
In this simplified diagram, many bridges and shafts and other details are omitted. The four triangular courtyards fit together to form a large interior square. The four bastions jut outwards in the four directions without ever actually touching the courtyards; in the space between, the four towers reach upwards. The four deeps, not shown in this sketch, lurk beneath the surface; I imagine them standing like pillars in an underground cavern.
Behind the walls and beneath the surface, over a thousand individual passageways, called crossings, follow the eight great horizontal and vertical circles of the torus. The great wall encircling the maze contains passages which lead from the North Bastion to the East, from East to South, from South to West, and back to North. Bridges (not shown) form similar circles, leaping from tower to tower and vaulting the separating walls between the courtyards.
Staircases wind up and down the center of each tower, connecting each courtyard to its tower and each tower to its bastion. More stairs plunge beneath the surface, connecting each bastion to its deep and its deep back up to its courtyard. Along the way, these various passages are forced to take many twists and turns, but beneath all this surface complexity lies the simplicity of a torus.
Inside Each House
The real complexity of the starmap lies not between the microcosms, but within them. In fact this is what made the starmap so hard to construct but so easy to read: the rooms inside each microcosm were arranged in a very special way, with many strangely twisting micropipes, for the sole purpose of making the movement between microcosms as simple as possible.Because of this special internal arrangement, any given pair of rooms connected by a macropipe occupy exactly the same position within their respective microcosms. So a room second from the left on the third row in one microcosm always leads to a room second from the left on the third row of a neighboring microcosm. This meant that I didn't have to draw the thousand individual pipes connecting the microcosms. To move between microcosms you just start in a room and move your finger in a straight line, up, down, left, or right, until it enters a single large pipe bundle. You follow that pipe to wherever it leads, then locate the room in the same position you started from.
Another powerful advantage of this system is that although the pipe colors varied from one microcosm to the next, the internal structure remained exactly the same:
While this arrangement perfectly suits the goals of the starmap, it has one profound disadvantage: it obscures the natural gradient within each microcosm from the dominant room to it's opposite. All motion within a microcosm starts from a dominant room, positioned differently in each case, and flows steadily down until it reaches a terminus. This pattern of change occurs so frequently in the starmaze that I have given it a name: the binary trickle.
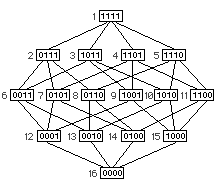 As you can see by the diagram at right, a binary trickle describes all the different paths
by which a binary coordinate can transform from all 1s to all 0s one bit at a time.
The four-bit trickle forms a tesseract; in four-dimensional space its 32 edges would all be straight
and all the same length. In three dimensions, we can intuitively represent the gradient
as a steady descent through five levels, but we are forced to break the perfect symmetry of
the nodes and severely bend some of the connecting edges:
As you can see by the diagram at right, a binary trickle describes all the different paths
by which a binary coordinate can transform from all 1s to all 0s one bit at a time.
The four-bit trickle forms a tesseract; in four-dimensional space its 32 edges would all be straight
and all the same length. In three dimensions, we can intuitively represent the gradient
as a steady descent through five levels, but we are forced to break the perfect symmetry of
the nodes and severely bend some of the connecting edges:
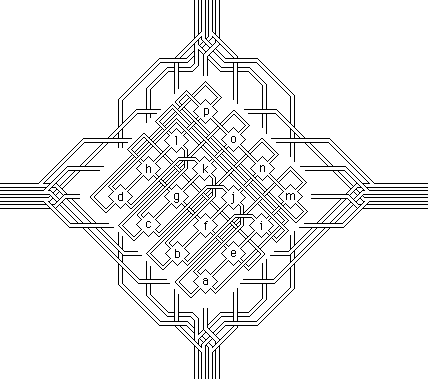
Most of the 16 rooms naturally gravitate to a symmetrical arrangement. Rooms 1 and 16 define the top and bottom of a central axis. The rooms on levels 2 and 4 spread out from the center to assume positions at the four points of the compass. Level 3 defines an equator with each room combining two of the four possible directions. Four of the rooms on level 3 (6, 7, 10, and 11) fit perfectly in the Northeast, Northwest, Southeast, and Southwest positions.
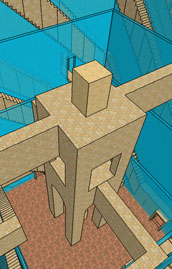 Rooms 8 and 9 are the trouble-makers. They correspond to the nonsensical positions of Northsouth and Eastwest.
As a result there is no completely harmonious way to position them in 3-space. They can't both
be at the center, so I either have to place them arbitrarily, split them into joined pairs like
intersecting barbells, or put them on their own separate levels. In the courtyard this forces a subtle
break in an otherwise mirror-image symmetry. In the tower, shown at right, I was forced to split
each room into connected pairs of chambers and place the intersections on separate levels,
creating a tower within the tower.
Rooms 8 and 9 are the trouble-makers. They correspond to the nonsensical positions of Northsouth and Eastwest.
As a result there is no completely harmonious way to position them in 3-space. They can't both
be at the center, so I either have to place them arbitrarily, split them into joined pairs like
intersecting barbells, or put them on their own separate levels. In the courtyard this forces a subtle
break in an otherwise mirror-image symmetry. In the tower, shown at right, I was forced to split
each room into connected pairs of chambers and place the intersections on separate levels,
creating a tower within the tower.
This 3D trickle, then, forms the basis of room arrangements within each house of the 3D starmaze. I place the first room at the top of each house (level 1), provide metal slides down to rooms 2 through 5 (level 2), and so forth. In this way I exploit the third dimension to emphasize the gradient within each house and use gravity to make the arrangement deeply intuitive.
The only other complication is that I have to fit the trickle pattern into the unique shape of each type of structure within the maze: bastions, towers, courtyards, and deeps. To do this, I make a few arbitrary decisions which quickly lead to a series of ever-more constrained decisions until I am essentially forced to create arrangements that would never have occurred to me otherwise. This is where the surprises come in and why I sometimes find myself standing in spaces I never before imagined.
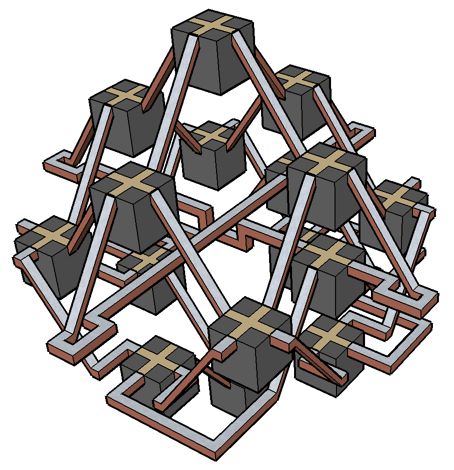
Here, for example, is the floorplan I developed for the four bastions:
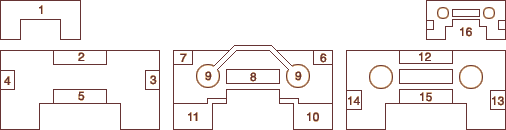
Room 1 is at the top, room 16 at the bottom. Rooms on the second and fourth levels are arranged around the points of a compass, but I had to displace rooms 13 and 14 to make room for crossings entering from the great wall. I placed room 8 in the center and for 9 did the next best thing: I split it and put half on either side of 8. To make room 9 visually distinct I rendered the two halves as cylinders then joined them together by creating a connected balcony. To connect room 8 to the great wall I was forced to drill tunnels through both cylinders. I then had to wrap more passages around the cylinders to connect room 8 with rooms 13 and 14.
Countless other problems had to be overcome one at a time, with each solution filling more of the available space and further constraining subsequent solutions until no choices were left and the rest of the bastion designed itself. Here's what it ended up looking like in 3D:
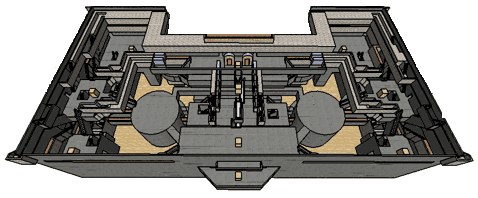
Once the model was fully built in Sketchup, I could walk through the tunnels, climb winding stairs, and leap from one platform to the next. I sometimes found myself standing in places I had not given much thought to when sketching the floorplan - like room 15, a solemn chamber at the base of a slide nestled between two overhead walkways that create a sense of shelter. Even before the furnishings are added (I imagine the East Bastion as a library worth of Borges, the West as a museum of time) the very shape of the surrounding structure lends each room a distinctive personality which has to be experienced to be fully appreciated. Click on the image above to experience a fly-through for yourself.
Crossings
Arranging the rooms of each house according to the binary trickle diagram has one distinct disadvantage. Because each house starts from a different dominant room, it is no longer obvious how the rooms connect when you cross from house to house. If you start at the top of the west tower and cross the bridge to the south tower you will wind up not in room 1, but in room 7 of all places. At first these movements seem random, but as always with the starmaze there is a pattern.
 To understand the way in which rooms change over crossings, you have to understand the way
the nine cells of the original puzzle are intertwined.
The identity of each house is determined by the shape (circle or square) of the four yin cells
in the four corners of each pattern. There are 16 possible combinations corresponding to the 16
possible house locations. Choosing a yin cell causes the shape of only that one cell to change,
moving the underlying binary address by one bit, and moving the location 90 degrees along one of
the horizontal or vertical circles of the torus. The northwest and southeast cells lead to horizontal
crossings; the northeast and southwest cells lead to vertical crossings.
To understand the way in which rooms change over crossings, you have to understand the way
the nine cells of the original puzzle are intertwined.
The identity of each house is determined by the shape (circle or square) of the four yin cells
in the four corners of each pattern. There are 16 possible combinations corresponding to the 16
possible house locations. Choosing a yin cell causes the shape of only that one cell to change,
moving the underlying binary address by one bit, and moving the location 90 degrees along one of
the horizontal or vertical circles of the torus. The northwest and southeast cells lead to horizontal
crossings; the northeast and southwest cells lead to vertical crossings.
Shifts within a house, which are made by choosing the yang cells, have no effect on the shape of yin cells - this is what makes a house a house. But movement through any yin cell causes the two nearest yang cells to flip states from filled (open) to empty (closed) or vice versa. And because position within a house is controlled by the state of yang cells, not the shape, this means that every crossing causes a change equivalent to two separate shifts.
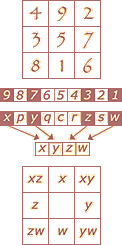 In order to figure out how we got from room 1 to room 7 we need to understand how room numbers
are assigned within each house, which in turn depends on how dimension numbers are assigned.
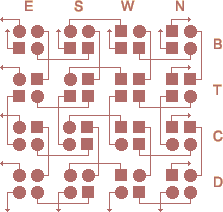
As shown in the diagram at right, the nine dimensions of a starmaze pattern are numbered according to
the Lo Shu. The yin cells have even numbers, the yang cells have
odd numbers with the fifth dimension reserved for the center. When plotting charts I usually use
the variable c for the center dimension;
p, q, r, and s for the yin dimensions;
and x, y, z, and w for the yang dimensions.
Each house is based on the four-bit binary trickle diagram using
the dimensions x, y, z, and w.
The left-most (most significant) bit represents dimension 9,
the next bit dimension 7, and so forth. This ordering is what causes the top to bottom, right to left
(instead of left to right) numbering in many parts of the various house blueprints.
In order to figure out how we got from room 1 to room 7 we need to understand how room numbers
are assigned within each house, which in turn depends on how dimension numbers are assigned.
As shown in the diagram at right, the nine dimensions of a starmaze pattern are numbered according to
the Lo Shu. The yin cells have even numbers, the yang cells have
odd numbers with the fifth dimension reserved for the center. When plotting charts I usually use
the variable c for the center dimension;
p, q, r, and s for the yin dimensions;
and x, y, z, and w for the yang dimensions.
Each house is based on the four-bit binary trickle diagram using
the dimensions x, y, z, and w.
The left-most (most significant) bit represents dimension 9,
the next bit dimension 7, and so forth. This ordering is what causes the top to bottom, right to left
(instead of left to right) numbering in many parts of the various house blueprints.
The resulting matrix shows how each yang cell maps to particular connecting lines in the binary trickle chart. It also shows which two yang cell shifts are associated with each yin cell (and thus with each crossing). All of this becomes more clear when the trickle chart is drawn to to look more like the tesseract that it is, with dimensions labeled, as is done in the following mandala-like diagram:
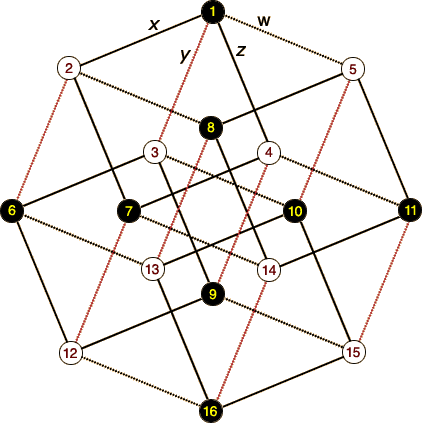
Rooms on odd levels are shown in black, even levels in white. Each yang movement corresponds to one of four types of lines (x, y, z, and w, each drawn in a consistent style and angle). For each room, lines coming in from above represent closed yang cells; lines going down represent open yang cells which lead to destination rooms.
Each yin movement corresponds to a type of square. A tesseract contains 4 xz squares, 4 yw squares, 4 xy squares, and 4 zw squares (among others). Yin movements result in room changes described by traveling halfway around each square (or flipping it if you prefer).
For example, there are four xz squares in the tesseract, corresponding to the northwest yin (cell 4). The first of these starts in room 1, flows down to either room 2 (along the x dimension) or room 4 (along the z dimension), then comes back together in room 7. Any movement through cell 4 will not only perform a horizontal crossing to an adjacent house, it will also cause every room number to flip to the opposite point in whatever xz square it belongs to. So if you start in room 1 at the top of the west tower and take cell 4 to cross over to the south tower, you will wind up in room 7 (just as if you had landed in room 1 and then shifted down both x and z lines in either order).
Likewise, if you started in room 2 you would flip to room 4 or vice versa. And the same is true for any other xz square: 8 flips to 11, 5 to 14, 6 to 9, etc. A subsequent horizontal crossing from the south tower to the east would involve cell 6 and thus the yw squares. Room 7 would flip to room 16. Vertical crossings cause rooms to flip along the xy squares (for cell 2) or the zw squares (for cell 8). All of these movements are summarized in the following pair of diagrams:
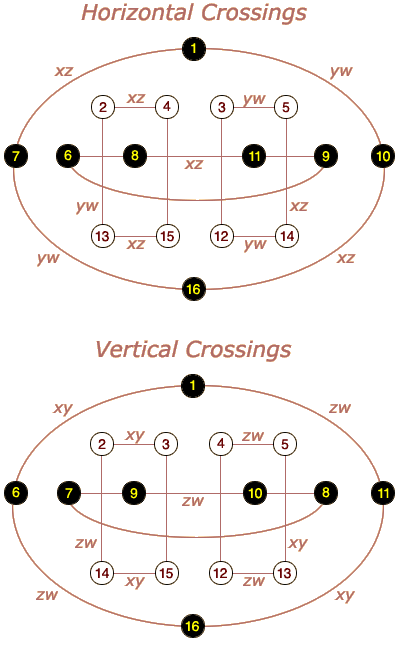
Each cycle through four rooms is accomplished by alternating back and forth between cells 4 and 6 (for horizontal crossings) or cells 2 and 8 (for vertical crossings); in practice, coming full circle requires 2 extra shifts along the way. Notice that rooms in odd levels only change to other rooms in odd levels, and the same for even levels. This means that the only way to move from an odd level to an even level or vice versa is by making a shift within a house via a yang cell.
Unlike 3D objects which rotate about lines, a tesseract can rotate about any one of six different planes (or can even rotate around two at once). So another way to think about these transformations is to imagine that the 16 xyzw-tesseract houses are arranged at the 16 corners of a super pqrs-tesseract (roughly corresponding to the key points around a torus) and that each house is also rotated 180 degrees relative to its four neighbors about one of four planes (movement through dimension r causes rotation around the xz plane, etc.). This is rather mind-bending (for me at least) but shows that the seemingly random permutations of room numbers actually arise in a very consistent way from the underlying geometry of the way houses are arranged in space.
Modeling these transformations require additional twists and turns throughout the crossings of the 3D starmaze. Transformations between bastions are done entirely within the great wall. Individual channels within the wall (arranged in two levels of eight channels each) dip and rise and switch back and forth like train tracks in a switching yard while the individual gradients of each channel are controlled by stairs and slides placed in a pavilion at each turning point of the wall. Bridges between towers have less space to work with, so control the gradients but leave the transformations to individual routing within the towers. Elsewhere each crossing is handled independently. Horizontal crossings at the fourth level of the deeps are handled by automated cockleshell boats.
Turning Inward
Alert readers will notice that I have dealt with the four yin cells and the four yang cells but have left one dimension untouched so far: the mysterious center dimension, dimension 5 in the Lo Shu. This is handled differently in the 3D starmaze than it is in the starmap.In the starmap, each diamond represents both a pattern and its inverse. This association is what allowed me to use pipe colors to eliminate thousands of little arrows on the map. It also allowed me to use a single pipe as both the entrance to and exit from the maze.
 The center dimension in the starmap is represented by a colored dot in the center of each diamond.
Like the macropipes connecting adjacent houses, the center dot symbolically represents movement through
a single large center-pipe bundle that always travels to an identical position in the most distant microcosm
(two over and two up), thereby eliminating the need to draw hundreds of center pipes to and from each room.
In the starmap, traveling through the center always involves a journey to a distant microcosm.
The center dimension in the starmap is represented by a colored dot in the center of each diamond.
Like the macropipes connecting adjacent houses, the center dot symbolically represents movement through
a single large center-pipe bundle that always travels to an identical position in the most distant microcosm
(two over and two up), thereby eliminating the need to draw hundreds of center pipes to and from each room.
In the starmap, traveling through the center always involves a journey to a distant microcosm.
The 3D starmap reverses this. It has no need for colored pipes and cannot rely on symbols and conventions; the passages must be as efficient as possible, but cannot be intangible. In the 3D starmap it is the the inverse of a pattern that is always located in the most distant house (two horizontal crossings and two vertical crossings away) while the journey through the center is as short as can possibly be: a quick transition through a hole in the floor or ceiling.
In fact, the two patterns connected through the center cell are considered to be two chambers of the same room. The upper chamber is called the "public" chamber and is always exposed to the open air. The lower or "private" chamber is always enclosed, without windows or natural light, and can only be reached via a secret passage concealed within a stone monolith that marks each room.
The overall effect is not unlike a recurring dream I sometimes have. In this dream I am wandering through a large but familiar structure, my childhood home or a rambling inn that I had been occupying for some time. In the dream I find a secret passage in some dusty basement, usually a tight crawl-way that seems ordinary at first. I push in to find first one secret room, and then another, and another. Gradually I realize that there is an entire house within a house, a secret house that I never knew existed.
So it is in the 3D starmaze. Not only is there a secret room concealed beneath each and every monolith, but every passage, every bridge and staircase, contains a secret passage running underneath. Those who have seen screenshots or movies of my Sketchup models, and who marvel at the sheer number of rooms and passages, are seeing only half of the maze. The other half, the private half, lies concealed beneath its floors.
There are many advantages to this system. In addition to being poetic, it is marvelously efficient. Because of the way the starmaze puzzle is defined, private passages map perfectly to public passages, both shifts and crossings. The passages (hallways, stairs, slides, bridges, etc.) all have to be thickened to hold an under-passage, but the total number is cut in half.
The explanation for this lies in the way the center interacts with the other cells. The chamber of a room is defined not by the state of the center cell, but by its shape: square for private, round for public; thus it is unaffected by movement through other cells. Choosing the center cell does not affect yin cells in any way, so the pattern of opened and closed crossings and destinations in a public chamber is identical to that of its private counterpart.
Movement through the center cell does affect the yang cells - in fact, it inverts them. But because this creates a perfect mirror image, shifts within a private house map perfectly to its public shifts. In the public half of a house, movement starts at the top and literally slides down to the bottom. The private half starts at the bottom and works its way up until it reaches the top. To accomplish this, a stairway is concealed beneath each slide with one-way doors on either end; once you start to climb a private stairway you cannot turn back.
As a result of the very different way that microcosms and houses are defined, only half of the patterns in a given microcosm reside in its corresponding house. Private chambers hold patterns from the corresponding microcosm; public chambers hold patterns from the opposite microcosm. The private starting pattern of the solution path lives in corresponding places (microcosm A in the starmap, east deep in 3D starmaze) while the public ending pattern lives in opposite places (microcosm A in the starmap, west tower in 3D starmaze).
 Movement between chambers in the 3D starmaze is accomplished via a secret passageway.
Every public room in the starmaze contains a stone monolith, five feet square and eight feet tall.
This monolith displays the starmaze pattern and other markings. If the center cell of that pattern is filled,
pushing it will open a narrow door.
Movement between chambers in the 3D starmaze is accomplished via a secret passageway.
Every public room in the starmaze contains a stone monolith, five feet square and eight feet tall.
This monolith displays the starmaze pattern and other markings. If the center cell of that pattern is filled,
pushing it will open a narrow door.
If this happens in a public chamber, the opened door reveals a fireman's pole. To reach this pole you must first enter the monolith, causing the weighted door to close behind you. When you reach the private chamber below you can push through a door at the base of the monolith which closes behind you and cannot then be reopened.
The other half of all open center passages start in the private chambers and move upward. Once again there are one-way doors at either end but in these rooms the central pole of the monolith supports a spiral staircase. You climb the stairs and push out to move from the dark world of the private maze to the public world of light above.
Because yang cell shifts affect neither the center cell's shape nor its state, all the center passages in a given house travel in the same direction. But every yin cell crossing to an adjacent house does flip the state of the center cell, thus flipping its direction.
So half of the houses, the houses with an even number of round or square yin cells, only allow movement from private up to public via the secret winding staircases. I call these female houses. The other half, those with an odd number of round or square yin cells, only allow downward movement via fireman's poles. I call these male houses. Each male house is surrounded by four female houses and vice versa. The female houses open outward and the male houses turn inward.
Thrones
The central organizing principle of the 3D starmaze is the five-level house in which public chambers trickle steadily downward and private chambers trickle steadily up, all based on movements through yang cells. But in a way this is unfair because yin cells trickle too.If you come to a pattern with four open yin (corner) cells, and resolve to move for a time only by choosing yin cells, the choices before you will narrow steadily down in exactly the same way that choices narrow within a house. But since these are yin cells, each movement will carry you to a different house, two horizontal crossings and two vertical crossings, leading you inexorably, regardless of order, to the opposite house from the one you started in. This pattern of choices forms an invisible, virtual house that stretches across five real houses.
This virtual trickle pattern is often a useful way to navigate the maze and understand its changing patterns. So even though yang cell shifts are the established way of trickling in the 3D starmaze, I needed a way of marking these virtual yin cell trickles as well.
Hence, the throne. A throne represents the top or "seat" of a virtual yin trickle pattern. It occurs whenever a pattern has four open yin cells. Since yin cells are not affected by movements through the center cell, a throne belongs to both the public and private chambers of whatever room it occurs in.
 There are 16 throne rooms scattered throughout the maze in a particular way.
Because yang cell shifts preserve parity (add or subtract 0 or 2 to the number of open yin cells),
a house which starts with an even number of yin cells will stay that way in every room.
Thus all even-numbered yin cell patterns occur in female houses
and all odd-numbered yin cell patterns occur in male houses.
And because a throne room with four open yin cells is an even-numbered pattern,
the 16 thrones occur only in female houses; each female house contains two throne rooms.
Only queens, not kings, sit on starmaze thrones.
There are 16 throne rooms scattered throughout the maze in a particular way.
Because yang cell shifts preserve parity (add or subtract 0 or 2 to the number of open yin cells),
a house which starts with an even number of yin cells will stay that way in every room.
Thus all even-numbered yin cell patterns occur in female houses
and all odd-numbered yin cell patterns occur in male houses.
And because a throne room with four open yin cells is an even-numbered pattern,
the 16 thrones occur only in female houses; each female house contains two throne rooms.
Only queens, not kings, sit on starmaze thrones.
The symmetry of the binary trickle causes the two throne rooms in every female house to occur in precisely opposite positions. This means that if one throne occurs in room n, the other will occur in room (17-n).
In order to make these thrones easier to remember and distinguish, I have assigned each throne a name which refers to the substance the throne is made of or in some cases the decorations with which it is crafted.
The five virtual levels in these virtual houses are given names instead of numbers. The room containing the throne itself is called the "seat". Crossings taken in any order lead to one of four rooms, each called a dais, then to one of six rooms, each called a step, then to one of four more rooms, each called a foundation, and finally to the terminus of the throne, always located in the opposite house from the seat. All of these rooms are said to bear "allegiance" to their throne. If I ever get around to interior decoration, I plan to mark this by placing appropriate ornaments of allegiance in every room.
Discoveries
The starmaze in general, and my attempt to build a realistic 3D starmaze in particular, has from the beginning been a ponarv, a project of no apparent redeeming value. I did not begin this project with the intention of discovering anything useful, but, as always happens, I have already learned a thing or two along the way, and by seeking nothing may accomplish much.The first insight is that empty buildings are mostly made of passages. I used to think of the starmaze as primarily a collection of rooms, each room having significant weight and volume. But as I toil away, laying virtual bricks one at a time, I find that my rooms are dwarfed by the vast network of stairs and bridges and hallways.
This might change once the rooms are filled with furnishings and bric-a-brac intricately arranged. But empty rooms are easily designed, easily made, and easily lost amidst all the little pieces needed to knit rooms together. Now as I hold the starmaze in my mind, I feel the weight of all those connecting pieces. To really see and understand any multi-room building, you have to see and understand how it is put together. Obvious in hindsight, but now I know it in my bones.
Starmaze passages consume more "psychological" space but, as it turns out, not more actual surface area. It is tedious to calculate the exact amount of square feet consumed by every twisting passage and staircase, but when I did a partial survey I was astonished to discover that the total surface areas of rooms and passages are roughly equal. There are rooms in the bastions that look like narrow shelves when seen from above, but which consume more square feet than the house I am currently living in. So a second insight is that psychological space and physical space are not at all the same.
I have also discovered that three-dimensional space is not as roomy as I thought. The footprint of the starmaze complex consumes about a million square feet. It reaches more than twenty stories into the air and burrows deep underground. Given all that, I assumed I would have no trouble weaving my passages without unwanted intersections.
I soon learned otherwise. It was often surprisingly hard to find a way to connect the rooms in the way required without collisions. I had to survey the scene from every angle, squeeze into tight corners, and come up with ingenious out-of-the-box solutions just to make one connection. I would then realize that three more connections had to be routed through the very space I had just filled so tightly. In some cases I was eventually forced to loosen my restrictions and allow passages to merge and split before arriving at their appointed monolith.
As mentioned above, the most pleasant surprise has been the way that even basic shapes and enclosures convey a sense of personality. Even without furnishings, each room in my Sketchup model has a distinctive "feel". We are deeply spatial creatures, and are hardwired not just to comprehend space with our heads but to feel it with our hearts. This "Feng Shui" is a real phenomenon which I could not have encountered through a purely mathematical model. It may prove useful as a way of adding further depth and meaning to the patterns of the maze.
In addition to these basic discoveries about the nature of space, I continue to have many small epiphanies about particular ways in which the starmaze functions. The more vivid visualizations afforded by the realistic 3D layout allow me work out many problems entirely in my head - which is exactly what I hoped would happen.
My goal now is to turn the starmaze into a "memory palace" so vivid that I will be able to calculate the shortest path between any two patterns by simply seeing the answer. The construction of memory palaces is a lost art; I hope the discoveries I am making about space and feelings and verisimilitude will help me find a way.
Stone Soup
In the classic Grimm Brothers tale, returning soldiers convince selfish villagers to share their food by telling them they are making "stone soup". They place a stone in a pot of water and start it boiling. One by one they get each suspicious villager to add an apparently inconsequential ingredient until a flavorful soup comes together that is more than the sum of its parts.I often think of the starmaze as a kind of stone soup. The "stone" is the basic mathematical structure which, glorious though it is, is really nothing more than a big square. To this sterile beginning I add a label to clarify a particular insight, and then another, inevitably using words as metaphors to convey each new concept. Though I try to use them carefully, each new word leaves behind a residue of excess meaning, rubbing off flavors and evoking associations the way all words do.
The corners of the stone become "houses" and acquire shapes (tower, bastion, courtyard, deep). Each shape moves in four directions and the directions acquire terrains (forest, desert, ocean, mountain). Their properties acquire labels, yin and yang, sun and moon, seasons, elements, forms. Each house gets its own name: darkness, sand, rumor, rain. Thrones appear of carnelian and iron, emerald and onyx. The more I look, the more I see. The more I see, the more new words I need. Monolith, oculus, trickle, microcosm, macropipe, dais, grotto, keeper, key, channel, crossroad, subway, temple, terminus.
It may turn out that the greatest power of the 3D representation of the starmaze is the net of meaning it creates through this gradual accumulation of terminology. Indeed, my next big project will be to finally assign names to each pattern. Before the advent of the 3D starmaze this process would have been entirely arbitrary, like naming the identical corners of a cube. But now that the rooms are coming into focus, and acquiring vivid detail and a myriad of associations, I hope the names will start to emerge on their own.
Meanwhile I will continue to stir the pot and see what develops.
For blueprints and details of each house, see House Charts.
For images and videos of the 3D starmaze, see Artwork.